损失函数清单

损失函数(Loss Function)用来估量模型的预测值 $\hat y = f(x)$ 与真实值 $y$ 的不一致程度。这里做一个简单梳理，以备忘。

回归问题

常见的回归问题损失函数有绝对值损失、平方损失、Huber损失。

绝对值损失

又叫做L1损失。

$$L(y, \hat y) = |y - \hat y|$$ $$MAE = \frac{1}{n} \sum_{i=1}^{n} |y - \hat y|$$

MAE一个问题是在 $y - \hat y=0$ 处不可导，优化比较困难。

平方损失

又称为L2损失。

$$L(y, \hat y) = (y - \hat y)^2$$ $$MSE = \frac{1}{n} \sum_{i=1}^{n}(\hat y - y)^2$$

MSE一个问题是对异常点敏感，由于平方的存在，会放大对异常点的关注。

Huber损失

相当于是L1和L2损失的一个结合。

$$L_{\delta}(y, \hat y) = \begin{cases} \frac{1}{2}(y - \hat y)^2, && for |y - \hat y| \le \delta \\ \delta |y - \hat y| - \frac{1}{2} \delta ^2, && otherwise \end{cases}$$

Huber损失是对上述两者的综合，当 $\mid y-\hat y\mid$小于指定的值 $\delta$ 时，变为平方损失，大于 $\delta$ 时，则变成类似于绝对值损失。即避免了在$\mid y-\hat y\mid$在0处不可导问题，也解决了其值过大对异常值敏感的问题。值得注意的是，该函数在$\delta$处连续。

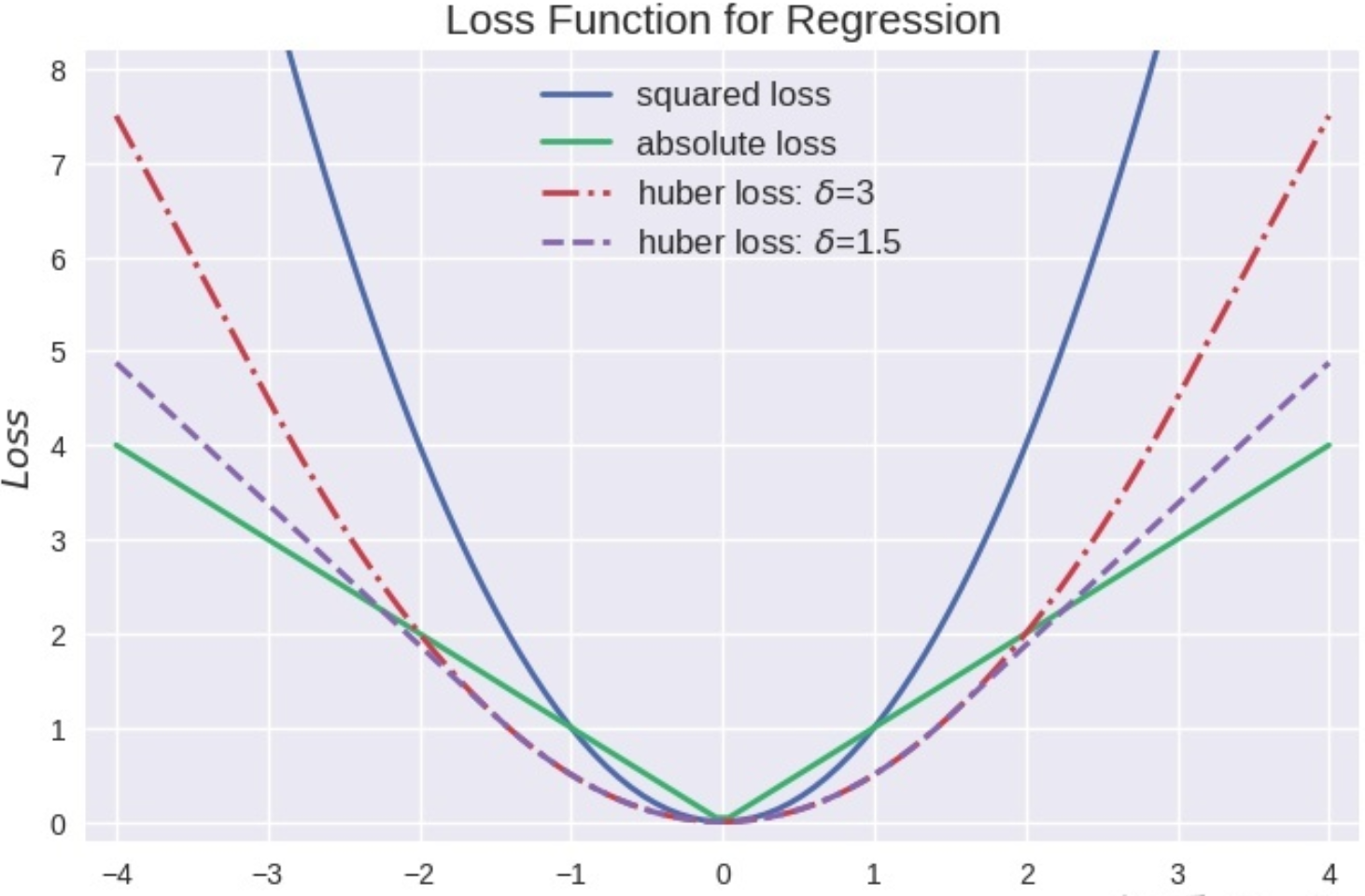
三种Loss随残差$\mid y-\hat y\mid$的大致走势如下图。

分类问题

一般来说，二分类机器学习模型输出有两个部分：线性输出$s$和非线性输出$g(s)$。其中，线性输出score一般是

$$s = w^Tx$$

非线性输出常见的如sigmoid：

$$g(s) = \frac{1}{1 + e^{-s}}$$

对应label $y$一般两种表示方式，${+1, -1}$或${1, 0}$表示正负类。其中用${+1, -1}$表示正类有个好处，就是从$ys$可以看出是否是误分类。

• 若$ys \ge 0$，则预测正确
• 若$ys \lt 0$，则预测错误

这样，$ys$和回归模型中残差$s - y$非常类似，以$ys$为自变量作图，方便理解。

0-1 Loss

0-1 Loss很直观，如果误分类则误差为1，否则为0。

$$L(y, s) = \begin{cases} 0, && ys \ge 0\\ 1, && ys \lt 0 \end{cases}$$

有两个明显的问题

• 0-1 Loss对每个误分类点惩罚相同，即使错的比较离谱(ys远小于0)
• 0-1 Loss不连续、非凸、不可导，梯度优化算法不适用

所以实际模型中0-1 Loss用的很少，后续介绍的误差，多数可看做0-1 Loss的一个上界。

Cross Entropy Loss

Cross Entropy Loss是非常重要的损失函数，也是应用最多的分类损失函数之一。根据label的表示方式，一般有两种常见形式。

如果label表示为${1, 0}$，形式如下：

$$L(y, \hat y) = -[ylog(\hat y) + (1 - y)log(1 - \hat y)]$$

简单看其来由。模型输出预测类别的概率

$$p = \begin{cases} p(y = 1|x) = \hat y \\ p(y = 0|x) = 1 - \hat y \end{cases}$$

以上可整合到一个公式中

$$p(y|x) = \hat y^y(1 - \hat y)^{(1 - y)}$$

根据极大似然估计原理，我们希望p越大越好，为了方便计算，同时引入负对数(不影响单调性)。

$$L(y, \hat y) = -log(p(y|x)) = -[ylog(\hat y) + (1 - y)log(1 - \hat y)]$$

其中

$$\hat y = \frac {1}{1 + e^{-s}}$$

代入可得出

$$L(y, \hat y) = \begin{cases} - log(\hat y) = log(1 + e^{-s}) && y = 1 \\ - log(1 - \hat y) = log(1 + e^s) && y = 0 \end{cases}$$

当y=1时，s越大loss越小；当y=0时，s越小loss越小，make sense。

如果label表示为${+1, -1}$，形式如下：

$$L(y, \hat y) = log(1 + e^{-ys})$$

其实上述式子完全等价，只不过将y=1或y=0两种情况整合到一起。ys的符号反映预测准确性，其数值大小反映预测置信度。

交叉熵损失在实数域内，Loss近似线性变化。尤其是当 ys « 0 的时候，Loss 更近似线性。这样，模型受异常点的干扰就较小。 而且交叉熵 Loss 连续可导，便于求导计算，应用比较广泛。

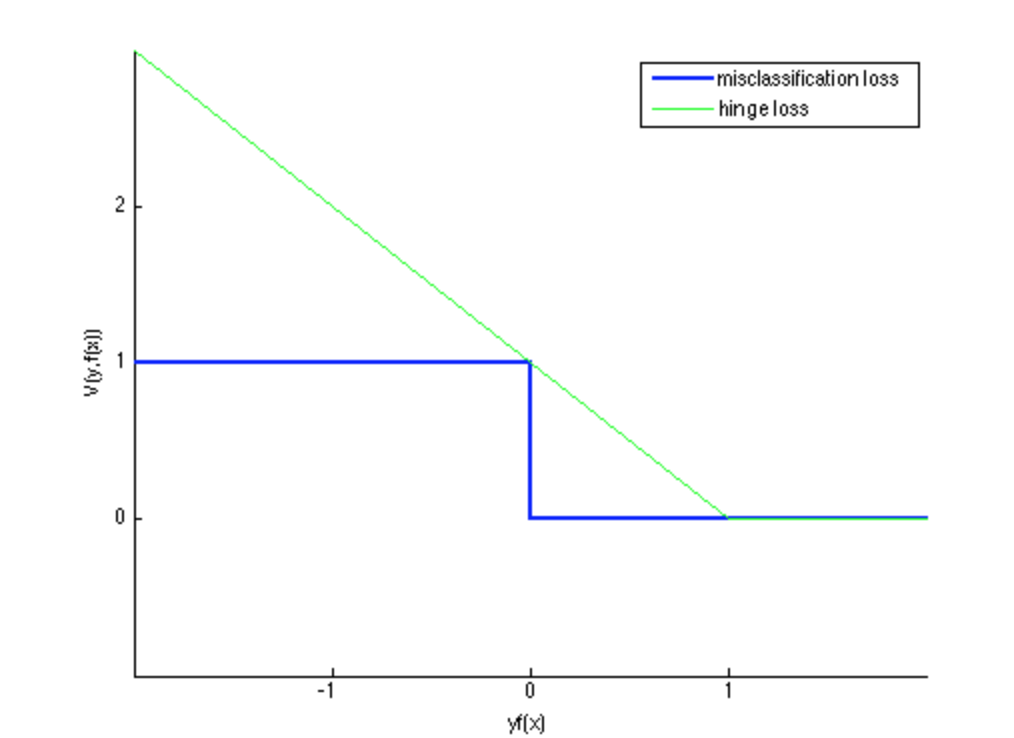
Hinge Loss

The hinge loss is used for maximum-margin classification, most notably for support vector machines (SVMs).

$$L(y, s) = max(0, 1 - ys)$$

Hinge Loss名字很象形，其形状类似合页。一般用于SVM中，体现SVM距离最大化思想。当Loss大于0时，是线性函数，可以用梯度优化算法。此外$ys > 1$损失皆为0，可以带来稀疏解，使得SVM仅通过少量支持向量就能确定最终超平面。

Exponential Loss

指数损失，多用于AdaBoost中，其它算法中用的较少。

$$L(y, s) = e^{-ys}$$

Modified Huber Loss

Huber Loss整合MAE和MSE的优点，稍作改进，同样可用于分类问题，称为Modified Huber Loss。

$$L(y, s) = \begin {cases} max(0, 1 - ys)^2, && ys \ge -1 \\ -4ys, && ys \lt -1 \end{cases}$$

该函数分三段

• $[-Inf, -1]$线性
• $[-1, 1]$二次
• $[1, Inf]$常数0

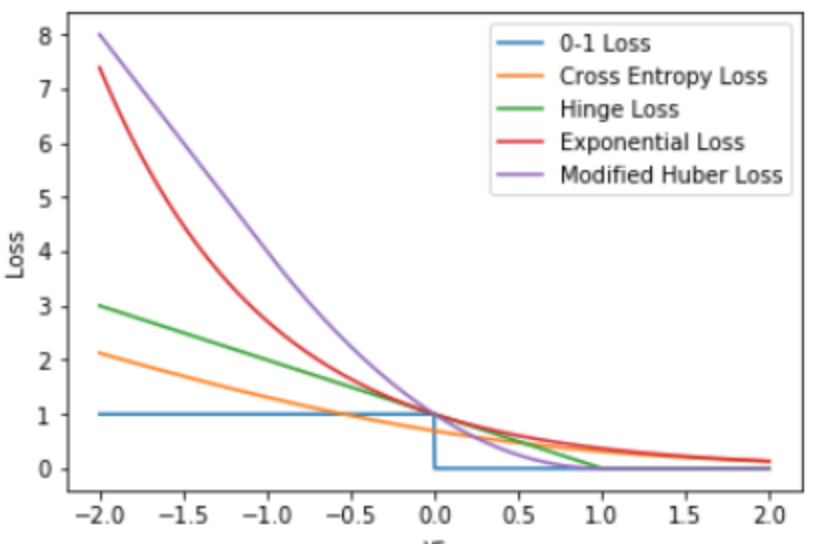
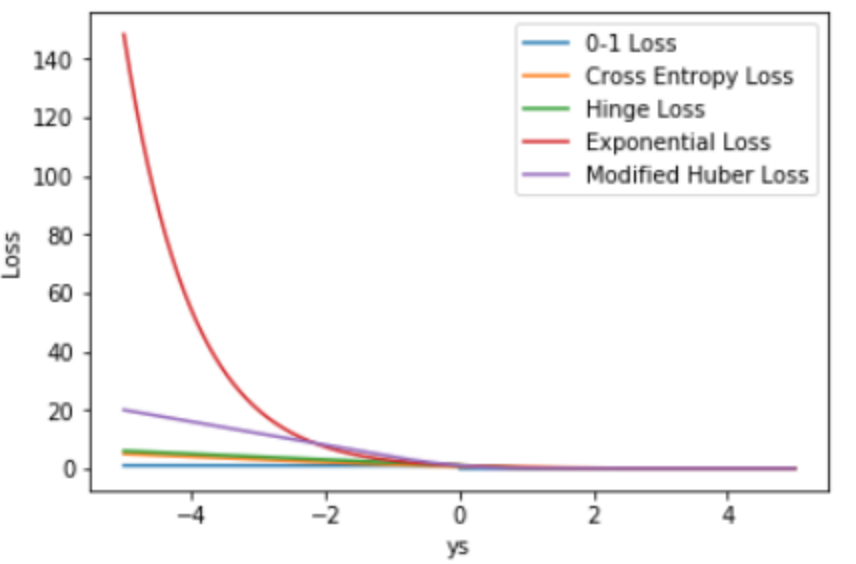
分类问题损失函数对比

对比不同损失函数随ys的变化趋势。有一点值得注意，就是各个损失函数在$ys$很小时，损失一般不超过线性（指数损失除外），否则对异常值太敏感。