PCA算法

PCA是一种很重要的降维方法，在数据压缩、可视化等领域应用广泛。在机器学习中，当特征维度过高时，可以选择Feature elimination或Feature extraction等方式降维。Feature elimination直接丢弃信息量低的特征，Feature extraction则从现有特征组合出一系列新特征，消除数据冗余，PCA数据Feature extraction。

经过PCA变换后：

• 变量之间互相独立
• 变量可解释性变差

算法步骤

1. 获取原始数据$X$，矩阵$m$个样本$n$个维度
2. 减去每一维均值$X_{adjusted}$
3. 计算协方差矩阵$C$，是对称矩阵
4. 计算$C$特征值和单位特征向量(其中一种方法)
5. 选取前$p$大特征值对应的特征向量组成
6. 对数据PCA变换

这样就将原始坐标系的向量，变换成新坐标系上的向量。

其中协方差矩阵的特征值分解

特征向量: The directions in which our data are dispersed.
特征值: The relative importance of these different directions.

超参选择

PCA降维，但如何确定保留多少维呢？除了拍一个值之外，还可以：

根据 proportion of variance explained，比如两个主成分对应的值

$$\frac{\lambda_1 + \lambda_2}{\lambda_1 + \dots + \lambda_n}$$

达到预期比如90%即可。

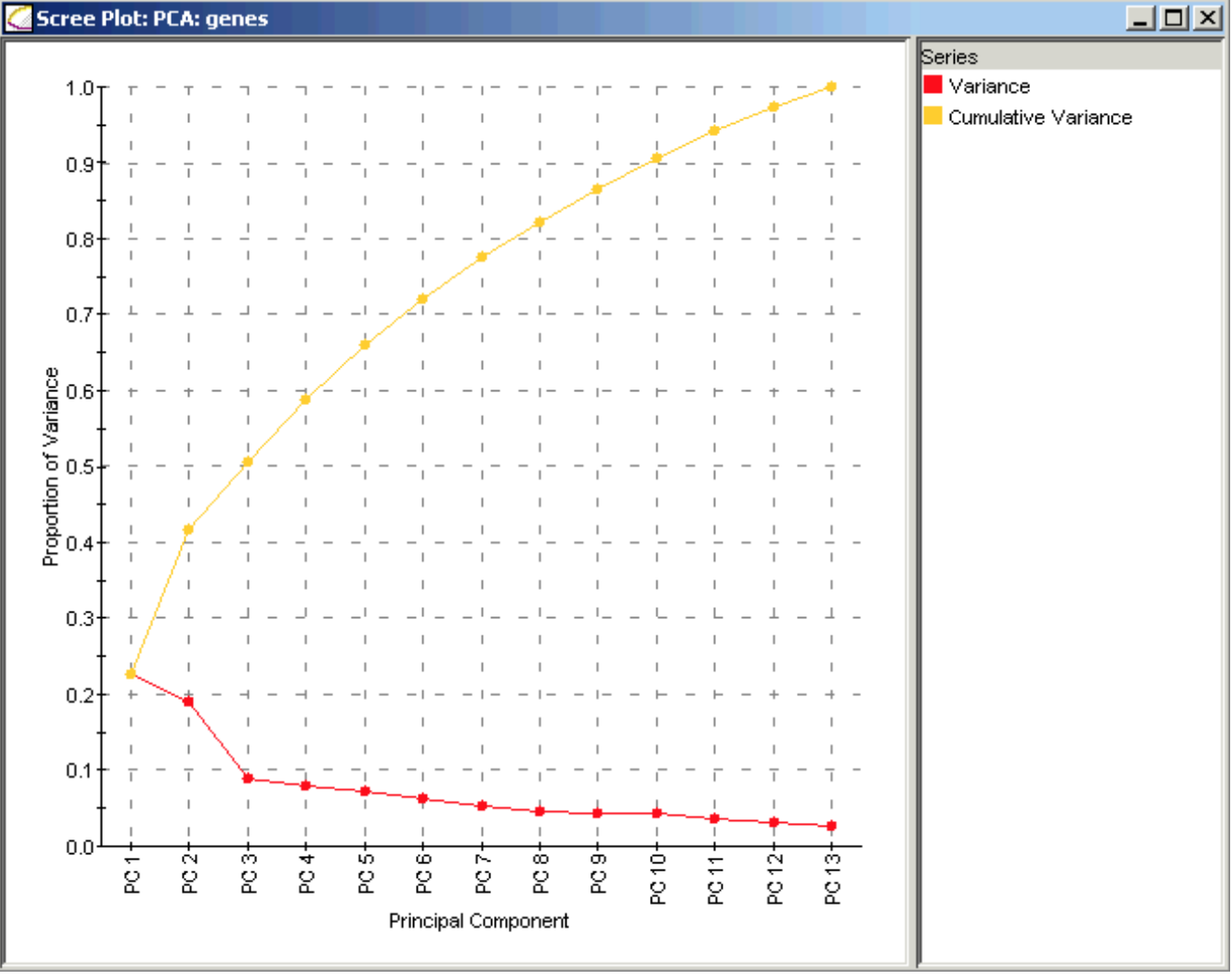
根据scree plot判断，又称为find the elbow当添加新的主成分时，variance变化剧烈时

Ref

• A Tutorial on PCA by Lindsay I Smith
• A Tutorial on Principal Component Analysis on arxiv
• A One-Stop Shop for Principal Component Analysis
• 如何解释协方差与相关系数
• 如何理解矩阵特征值？

Appendix

方差

方差(variance)用于衡量随机变量与数学期望之间的偏离程度。公式如下

$$var(X) = \sigma^2 = \frac{\sum_{i=1}^{n} (X_i-\bar X)^2}{n-1}$$

协方差

协方差衡量两个随机变量之前的相关性。通俗理解为两个变量在变化过程中是同向变化？还是反向变化？同向或者反向的程度如何？

• X越大Y也越大，X越小Y也越小，称为“正相关”
• X越大Y却越小，X越小Y却越大，称为“负相关”
• 既不是X越大Y也越大，也不是X越大Y反而越小，称为“不相关”

$$cov(X, Y) = \frac{\sum_{i=1}^{n}(X_i - \bar X)(Y_i - \bar Y)}{n-1} = E[(X-\bar X)(Y - \bar Y)]$$

协方差矩阵

协方差衡量两个变量之间的相关性，多个变量之间相关性可以放在矩阵中表示。矩阵中对角元素是每个变量的方差，且矩阵对称。

$$C= \begin {bmatrix} cov(x,x) & cov(x,y) & cov(x,z) \\ cov(y,x) & cov(y,y) & cov(y,z) \\ cov(z,x) & cov(z,y) & cov(z,z) \end {bmatrix}$$

相关系数

用XY的协方差除以X的标准差和Y的标准差。可以看成一种剔除了两个变量量纲影响，标准化之后的特殊协方差，可以更准确地反映两个变量每单位变化的相似程度。

$$\rho = \frac{cov(X,Y)}{\sigma_X \sigma_Y}$$

特征值和特征向量

$$Ax = \lambda x$$

左乘方阵表示空间的线性变化（旋转和拉伸）。由上式可得出几点结论

• $x$在$A$的作用下，保持方向不变，进行比例为$\lambda$的伸缩
• 特征向量所在的直线包含所有特征向量，称之为特征空间

矩阵可以利用特征值和特征向量实现对角化（须存在n个线性无关特征向量）

$$A = S\Lambda S^{-1}$$

其中$S$是特征向量矩阵，$\Lambda$是特征值对角矩阵。证明相对简单

$$AS = A \begin {bmatrix} | & | & | \\ x_1 & \dots & x_n \\ | & | & | \end {bmatrix} = \begin {bmatrix} | & | & | \\ \lambda_1x_1 & \dots & \lambda_nx_n \\ | & | & | \end {bmatrix}$$

而

$$\begin {bmatrix} | & | & | \\ \lambda_1x_1 & \dots & \lambda_nx_n \\ | & | & | \end {bmatrix} = \begin {bmatrix} | & | & | \\ x_1 & \dots & x_n \\ | & | & | \end {bmatrix} \begin {bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end {bmatrix} = S\Lambda$$

则

$$AS = S\Lambda$$

SVD分解

奇异值分解将矩阵分解成若干个秩一矩阵之和，用公式表示

$$A = \sigma_1\mu_1v_1^T + \dots + \sigma_r\mu_rv_r^T$$

且奇异值$\sigma$满足等式

$$\sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_r \gt 0$$

奇异值往往对应着矩阵中隐含的重要信息，且重要性和奇异值大小正相关。每个矩阵$A$都可以表示为一系列秩为1的小矩阵之和，而奇异值则衡量了这些小矩阵对于$A$的权重。小矩阵越多，其值越逼近原始矩阵$A$。

SVD的几何含义可解释为对任何一个矩阵，我们要找到一组两两正交单位向量序列，使得矩阵作用在此向量序列上后得到的新向量序列依然保证两两正交。奇异值的几何含义就是变化后新的向量序列长度。