决策树算法

关于经典决策树算法ID3、C4.5及CART树的部分细节梳理。

决策树

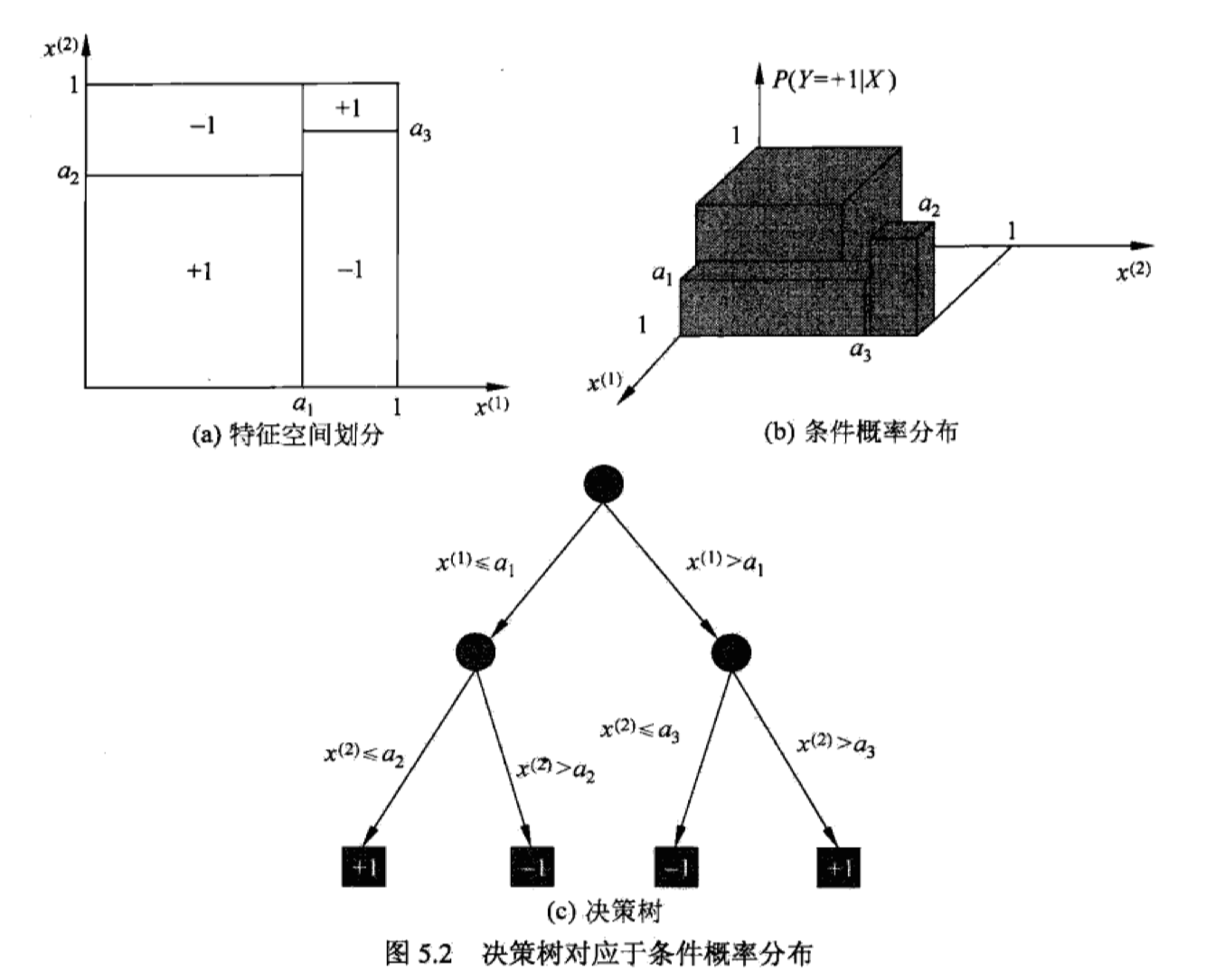
决策树可以从两个视角理解。

• If-Then规则的集合
• 定义在特征空间与类空间上的条件概率分布

经典决策树对比

经典决策树有ID3、C4.5以及CART树，其功能和学习过程各有异同，简单对比。

算法	分裂标准	树类型	特征类型	缺失	剪枝	任务
ID3	信息增益	多叉	离散	No	无剪枝	分类
C4.5	信息增益比	多叉	离散/连续	Yes	有剪枝	分类
CART	基尼系数	二叉	离散/连续	Yes	有剪枝	分类/回归

一些其它差异

• C4.5优化ID3，主要体现在节点分支计算方式，解决ID3偏向取值较多的属性
• 特征使用，多分的ID3和C4.5分类变量只使用一次，CART可多次使用
• CART回归任务，用平方误差最小准则选特征，用样本点均值做回归预测值

C4.5如何处理连续特征

连续值不再有限，不能直接取其可能取值划分，可采用二分法(bi-partition)。给定样本集$D$和连续属性$a$，其有$n$个不同取值，从小到大排序得${a^1, a^2, \dots, a^n}$，则划分点可以依次选取测试

$$T_a=\big\{\frac{a^i + a^{i+1}}{2}|1\le i\le n-1\big\}$$

注意，与离散属性不同，若当前节点划分属性为连续特征，该属性还可作其为后代节点的划分属性。

如何剪枝

一般分为预剪枝和后剪枝两种。

• 预剪枝：决策树生成过程中，在节点划分前评估，若当前节点划分不能带来泛化性能提升，则停止划分并将当前节点标记为叶子节点
• 后剪枝：对完全生长的决策树，自底向上对非叶子节点考察，若将节点对应子树替换为叶子节点能带来泛化性能提升，则将子树替换为叶子节点

预剪枝降低过拟合风险，基于“贪心思想”，也会带来欠拟合的风险；后剪枝欠拟合风险小，但训练时间开销比未剪枝或预剪枝大的多。

如何处理缺失值

在XGBoost里，做法是这样的。在每个节点上都会将含缺失值样本往左右分支各倒流一次，然后计算对Objective的影响，选效果好的方向，作为缺失值应该流向的方向。

比如特征A(A>0或A<=0或A=null)，那么首先忽略含缺失值样本，正常样本导流到到左子树与右子树；将含缺失值样本导向左子树，计算Objective_L；将含缺失值样本导向右子树，计算Objective_R。选择Objective较小的方向，作为缺失值应该分流的方向。

树何时终止生长

常见的几种终止条件有

• 叶子节点里样本类别都相同
• 叶子节点里样本数量少于某下限
• 树高度达某上限
• 分裂收益低于某下限
• 没有更多特征

附录信息

信息熵，表示随机变量的不确定性。

$$H(p) = -\sum_{i=1}^n p_ilog(p_i)$$

其中

$$0 \le H(p) \le log(n)$$

条件熵，表示在已知随机变量$X$的情况下$Y$的不确定性。

$$H(Y|X) = \sum_{i=1}^n p_i H(Y|X=x_i)$$

其中

$$p_i = P(X = x_i), i=1,\dots, n$$

信息增益，表示得知特征$X$的信息使$Y$不确定的减少程度。熵$H(Y)$与条件熵$H(Y \mid X)$之差称为互信息。决策树学习中的信息增益等级于训练数据集中类与特征的互信息。

$$g(D, A) = H(D) - H(D|A)$$

信息增益比，考虑信息增益相对值。训练数据经验熵较大时，信息增益偏大；信息增益偏向特征类别较多的特征。信息增益比有所矫正。

$$g_R(D, A) = \frac{g(D, A)}{H_A(D)}$$

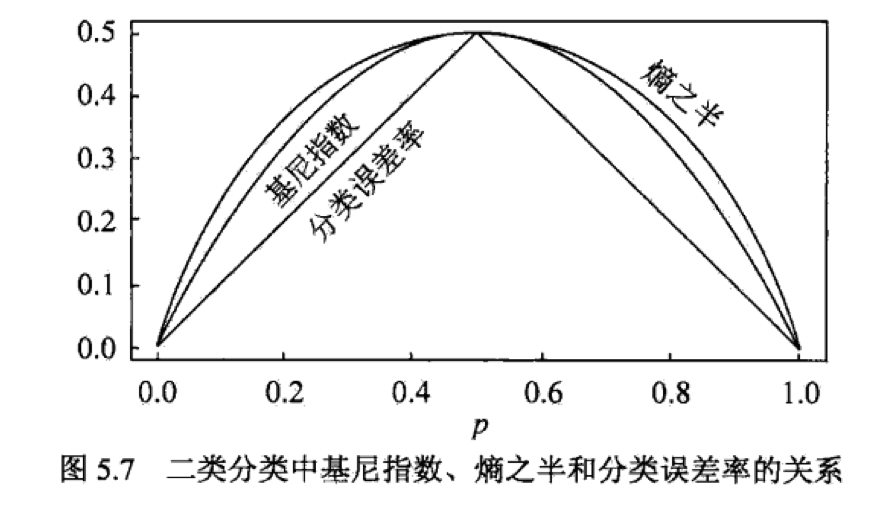
基尼系数，表示一个随机变量变为其对立事件的概率，也可以衡量随机变量的不确定性。

$$Gini(p) = \sum_{k=1}^K p_k(1-p_k) = 1 - \sum_{k=1}^K p_k^2$$

如图，基尼系数和熵之半很接近，都可以近似代表分类误差率。