逻辑回归为何不用平方误差

逻辑回归是经典的机器学习算法，其损失函数为交叉熵，但为何不用平方误差呢？本文从收敛速度角度简要介绍。

逻辑回归形式为

$$\hat y = \sigma(z) = \frac{1}{1 + exp(-w^Tx)}$$

交叉熵和平方误差损失函数分别为

$$L_{xent}(w,b)=-[yln\hat y + (1-y)ln(1-\hat y)]$$ $$L_{square}(w, b)=\frac{1}{2}(\hat y - y)^2$$

对参数$w_i$求导，交叉熵和平方误差对应梯度分别为

$$\frac{\partial L_{xent}(w,b)}{\partial w_i} = (\hat y - y)x_i$$ $$\frac{\partial L_{square}(w, b)}{\partial w_i} = (\hat y - y) \frac{\partial \hat y}{\partial w} = (\hat y - y)\hat y(1-\hat y)x_i$$

从上式可以看出，预测误差$\hat y - y$越大，交叉熵损失对应梯度越大，参数更新也就越快，能更快的收敛；但平方误差对应梯度中有一项$\hat y(1-\hat y)$

$$\frac{\partial\hat y}{\partial z}=\sigma'(z)=\sigma(z)(1-\sigma(z))=\hat y(1-\hat y)$$

观察上式有一些特点

• 当$y=1$, 若$\hat y$趋于1(close to target),梯度趋近于0，合理
• 当$y=1$, 若$\hat y$趋于0(far from target),梯度趋近于0，不合理
• 当$y=0$, 若$\hat y$趋于1(far from target),梯度趋近于0，不合理
• 当$y=0$, 若$\hat y$趋于0(close to target),梯度趋于0，合理

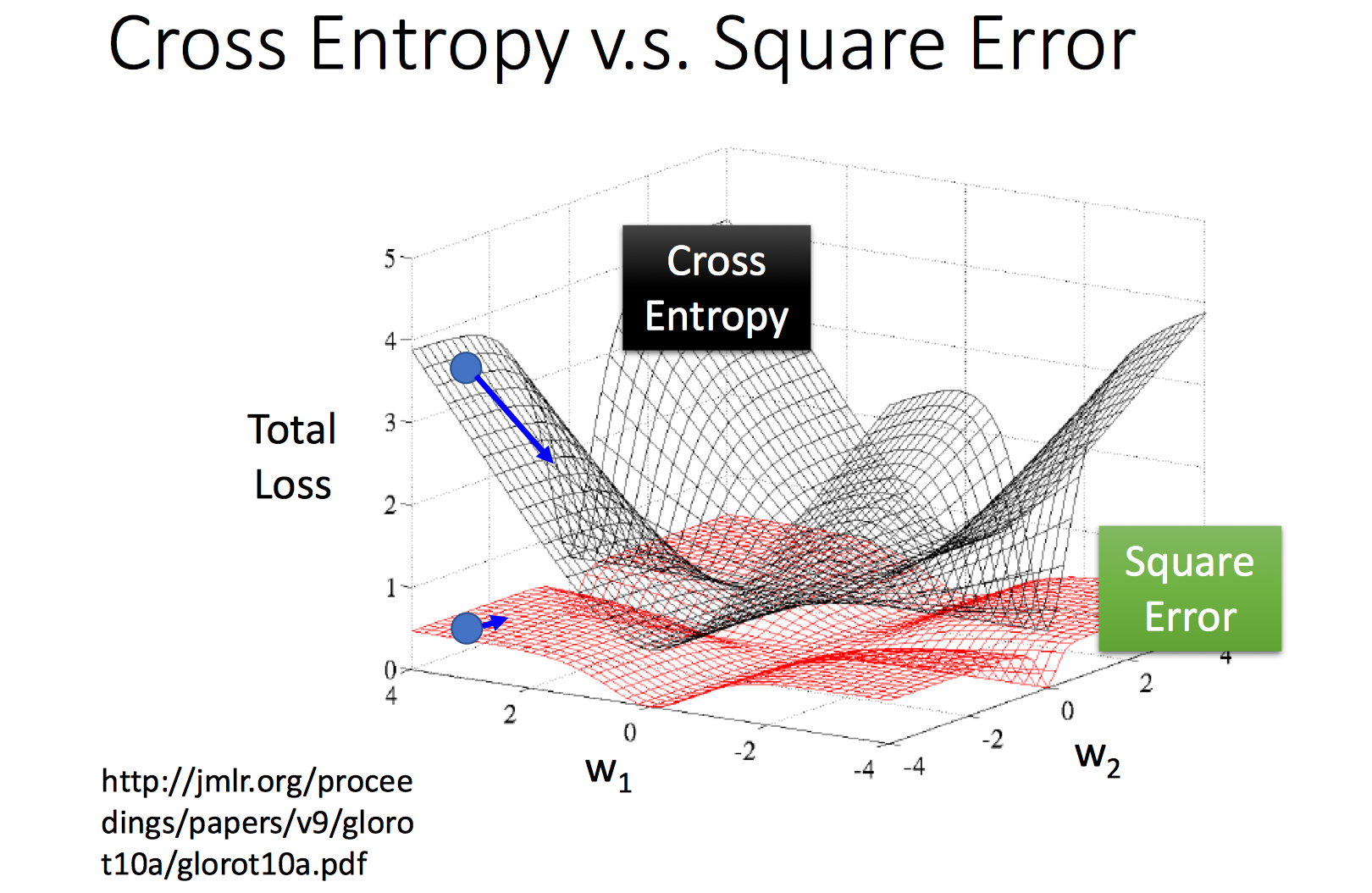
即当误差较大时，梯度值反而可能很小，导致难以收敛。如下图所示，当参数值离解位置较远时，平方误差其函数值比较平坦，梯度基本为0，导致学习非常缓慢，而交叉熵离解较远的位置，梯度较大。从学习速率角度看，交叉熵损失比平方损失更适合逻辑回归。