Bias和Variance

Published: 02 Jun 2019 Category: algo

机器学习模型的误差源于两部分Bias以及Variance，对其直觉的理解，有助于帮助找到模型优化的方向。

理想情况是Bias和Variance都很小，但实际情况二者经常是矛盾的，常常要在Bias和Variance之间做一个trade off，机器学习任务中到处都能看到bias and variance trade off。

先看其定义

偏差Bias：由所有采样得到的大小为$m$的训练数据集训练出的所有模型的输出的平均值与真实模型输出之间的偏差。

相应的，Variance的定义为

方差variance：由所有采样得到的大小为$m$的训练数据集训练出的所有模型输出的方差。

如下图，我们用100组训练数据，用相同的模型假设训练100个模型「最终参数不同」，其结果如图，则不同模型的输出均值即为Bias，方差即为Variance。

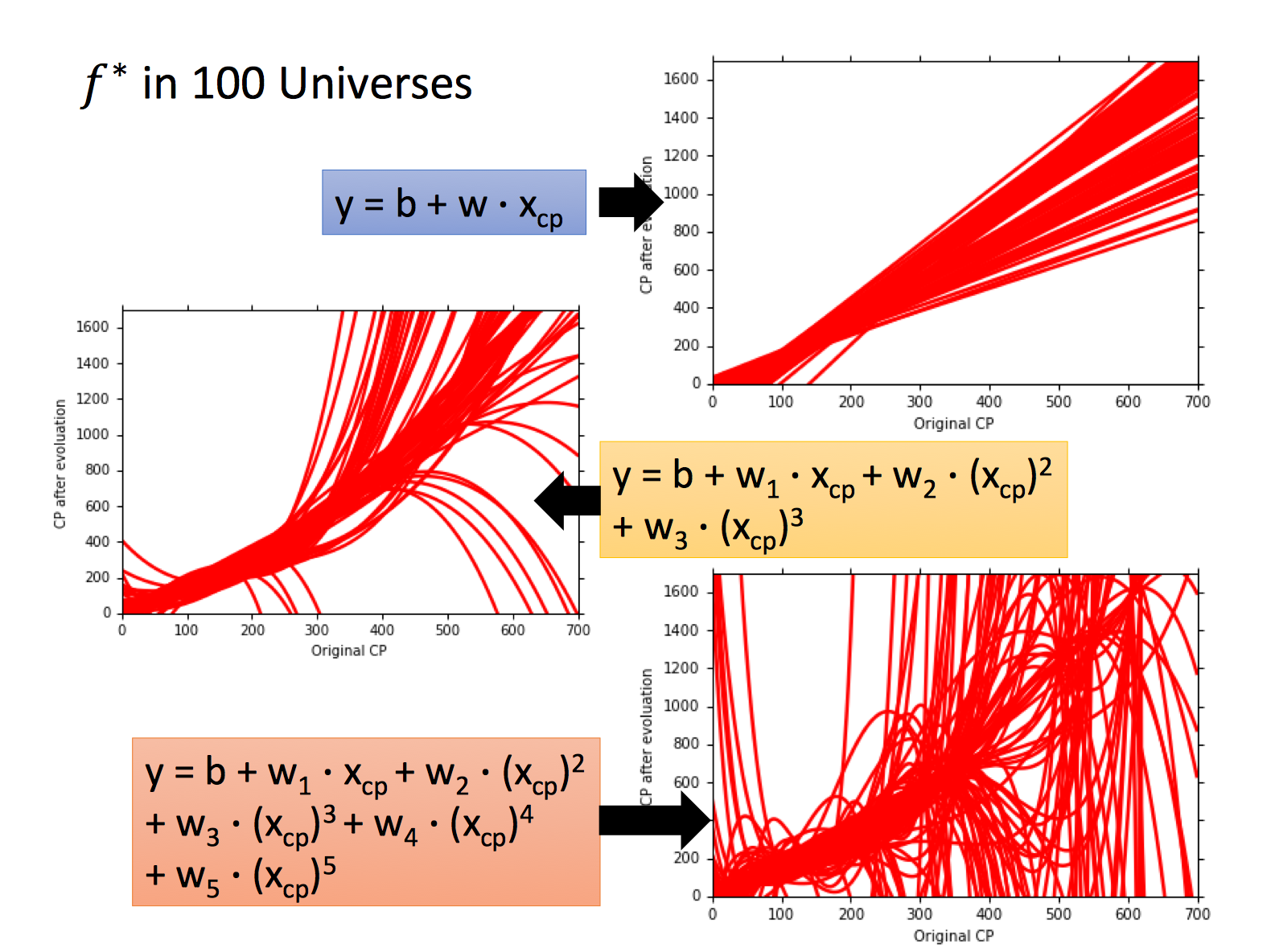
algo-bias-and-variance-Parallel-universes

如果将每一个模型输出比喻做一次涉及，其在靶子上的分布可以类比，来看如下经典的图

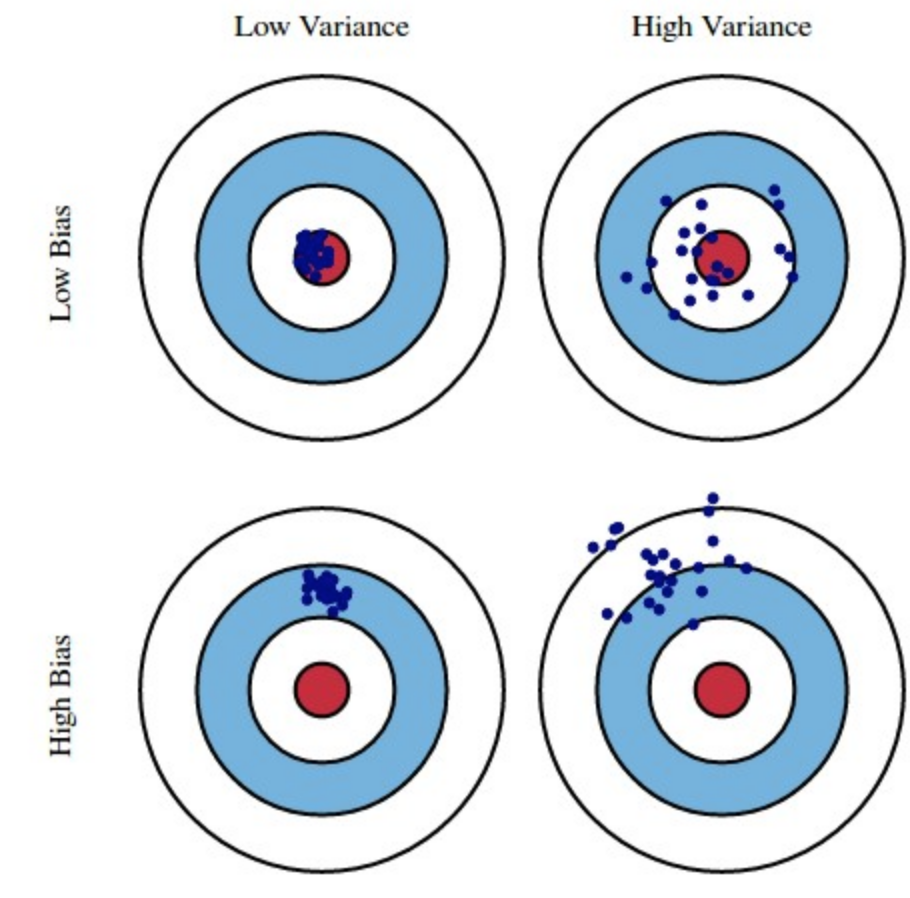
algo-bias-and-variance-target

$Error = Bias + Variance$

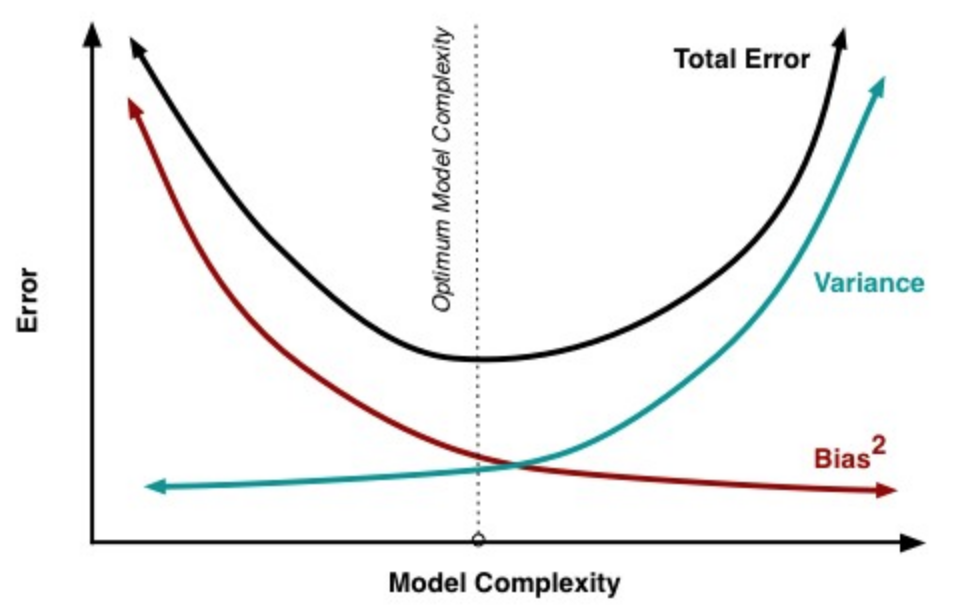
Bias大通常是对学习算法做出错误假设导致的，比如真实模型是二次函数，但我们假设模型为一次函数；往往体现在训练误差上；一般模型复杂度越高，偏差越小。

Variance通常由于模型复杂度相对于训练样本数$m$过高导致的，比如一共100个训练样本，而我们假设模型的是阶数不大于200的多项式函数；往往体现在测试误差相对于训练误差的增量上；一般模型复杂度越高，方差越大。

Bias和Variance随模型复杂度增加的典型表现如下图

algo-bias-and-variance-trade-off

那么Bias较大或者Variance较大时我们能做什么？

algo-bias-and-variance-reduce-bias

Bias大可能是规律未学到，也许信息未包含在数据中，这种情况可以找更多维度特征补充信息；也许是信息足够，但模型capacity不足，包含这些信息，这种情况可以加大模型capacity。

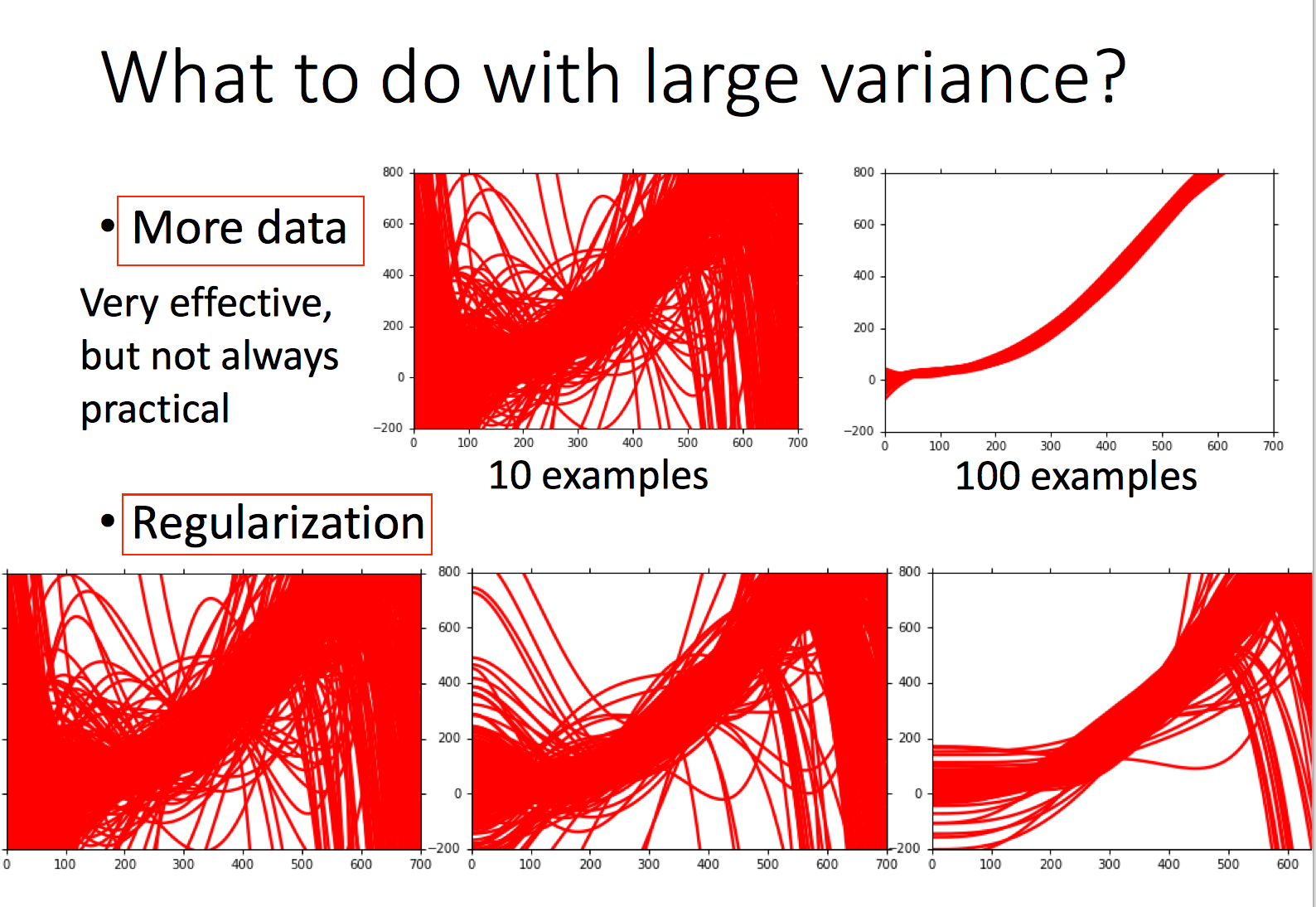
algo-bias-and-variance-reduce-variance

Variance大典型的可以通过增加数据和正则来缓解，不过还有其它很多手段减少模型过拟合。