10 Logistic Regression

介绍Logistic Regression算法，见详细课件。

Formulation

从分类（离散的）样本数据中学习这样一个目标函数

$$f(x) = P(+1|x) \in [0,1]$$

注意是概率（连续的）。相当于用分类的数据，学习回归函数。

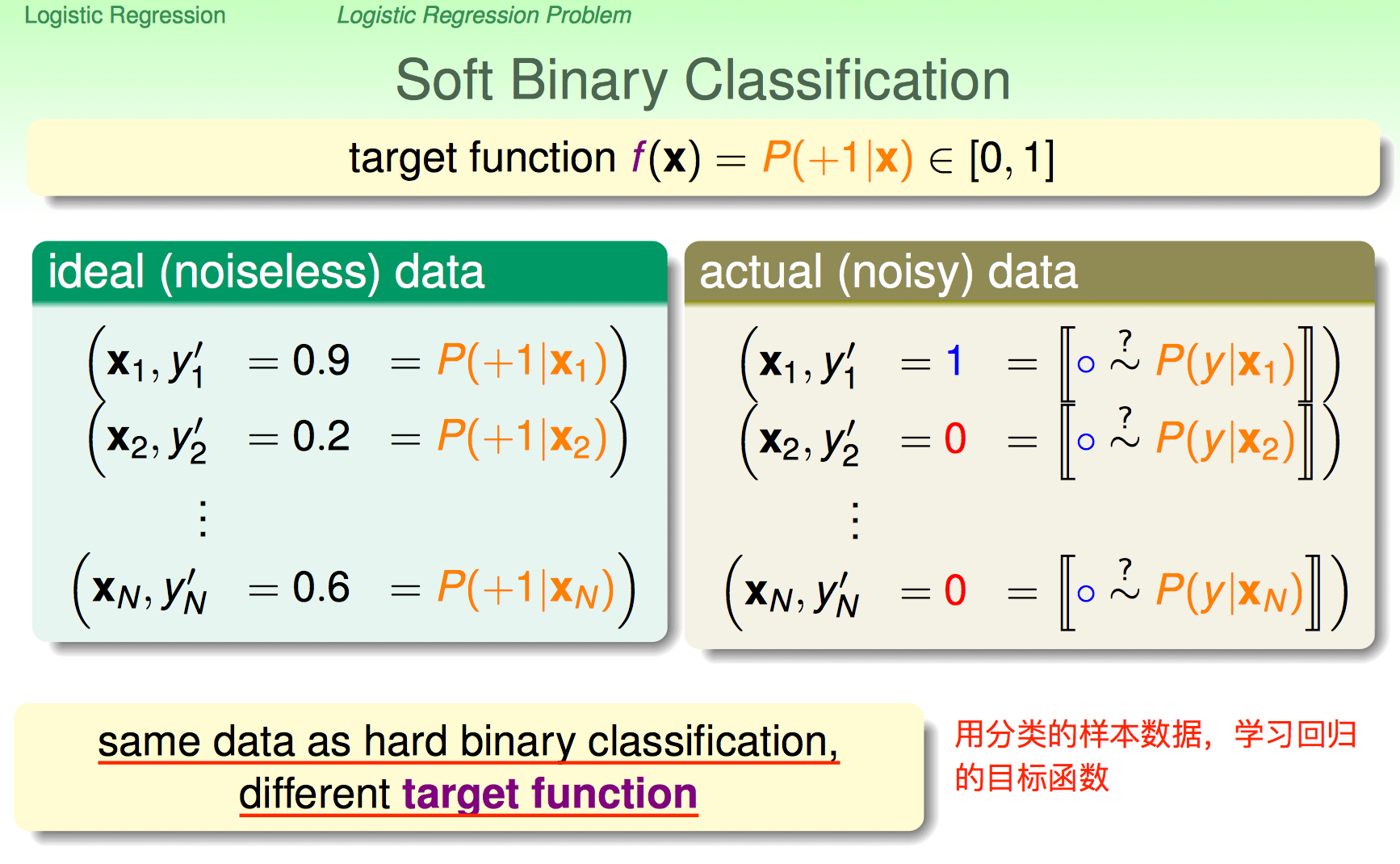
摘自教材《Learing From Data》

Formally, we are trying to learn the target function

$$f(x) = P(+1|x) \in [0,1]$$

The data does not give us the value of $f$ explicitly. Rather, it gives us samples generated by this probability, e.g., patients who had heart attacks and patients who didn’t. Therefore, the data is in fact generated by a noisy target distribution.

$$\begin{equation} P(y|x)=\left\{ \begin{aligned} &f(x) &&\text{for}\ y=+1 \\ &1-f(x) &&\text{for}\ y=-1 \end{aligned}\right. \end{equation}$$

问题可以抽象为，对输入

$$x=(x_0,x_1,x_2,\dots,x_d )$$

计算其weight score，与PLA和Linear Regression一样

$$s = \sum_{i=0}^{d}w_ix_i$$

然后经过logistic function将其转化为概率。简言之，逻辑回归就是用

$$h(x)=\frac{1}{1+exp(-w^Tx)}$$

来学习target distribution

$$\begin{equation} P(y|x)=\left\{ \begin{aligned} &f(x) &&\text{for}\ y=+1 \\ &1-f(x) &&\text{for}\ y=-1 \end{aligned}\right. \end{equation}$$

Likelihood

逻辑回归的Error Measure基于最经典likelihood的概念。即假设分布式是

$$\begin{equation} P(y|x)=\left\{ \begin{aligned} &h(x) &&\text{for}\ y=+1 \\ &1-h(x) &&\text{for}\ y=-1 \end{aligned}\right. \end{equation}$$

那当前样本集的likelihood为

$$\prod_{n=1}^NP(y_n|x_n)$$

使其最大化，对应的参数即我们期望的解。根据sigmoid函数性质（见附录），我们的假设分布可简化为（极其重要）

$$P(y|x)=\theta(yw^Tx)$$

将问题转化为求最小值（误差最小思路）

$$-\frac{1}{N}ln(\prod_{n=1}^NP(y_n|x_n))=\frac{1}{N}\sum_{n=1}^N ln(\frac{1}{P(y_n|x_n)})$$

得到优化目标为

$$\begin {align} E_{in}(w) &=\frac{1}{N}\sum_{n=1}^N ln(\frac{1}{P(y_n|x_n)})\\ &=\frac{1}{N}\sum_{n=1}^N ln(\frac{1}{\theta(y_nw^Tx_n)})\\ &=\frac{1}{N}\sum_{n=1}^N ln(1+e^{-y_nw^Tx_n}) \end {align}$$

可以看出，误差函数跟交叉熵（见附录）是等价的。得到误差函数之后，对其求导，即可用梯度下降或随机梯度下降求导。

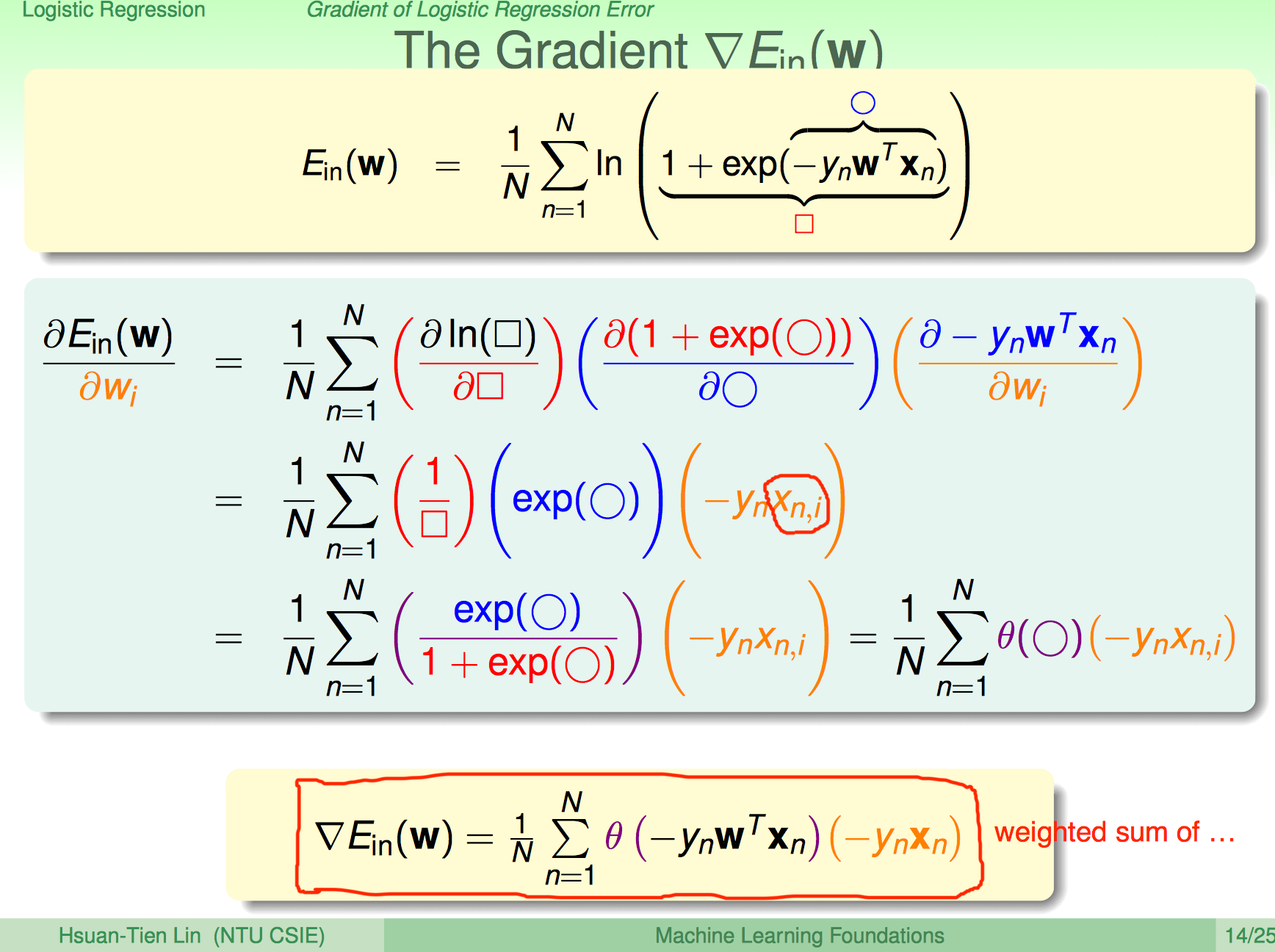
附录

Sigmoid

$$\theta(s) = \frac{e^s}{1+e^s} = \frac{1}{1+e^{-s}}$$

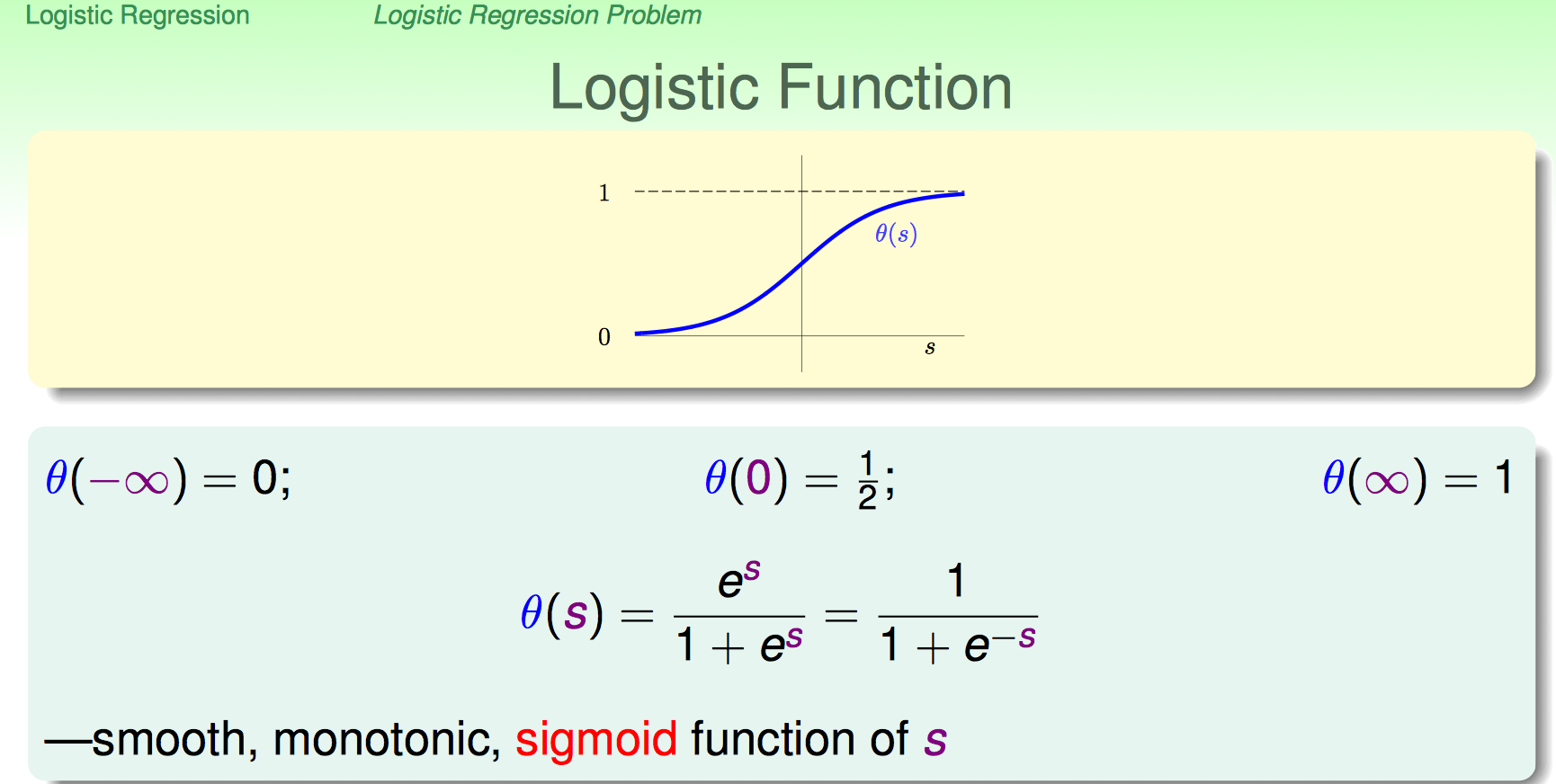
从图中对称性不难得出

$$\theta(-s) = 1 - \theta(s)$$

对其求导

$$\theta(s)'=\theta(s)(1-\theta(s))$$

与tanh函数关系（通过取值区间猜想）

$$tanh(s)=2\theta(2s)-1$$

其中 $tanh(s)=\frac{e^s-e^{-s}}{e^s+e^{-s}}$

交叉熵

两个概率分布${p,1-p}$以及${q,1-q}$，其交叉熵为：

$$plog(\frac{1}{q}) + (1-p)log(\frac{1}{1-q})$$