09 Linear Regression

介绍了线性回归算法，问题的解以及泛化误差分析，见详细课件。

关注几个核心问题：

• 问题的Formulation
• 最小二乘求解步骤
• 算法Intuition
• 误差公式推导以及泛化问题

Formulation

线性回归问题Formulation是，假设输入空间为

$$x = (x_0, x_1, x_2, \dots, x_d)$$

linear regression hypothesis为

$$y \approx \sum_{i=1}^d w_i x_i$$

即

$$h(x) = w^Tx$$

求解目标是使$E_{in}(w)$最小，其表达式如下

$$E_{in}(w) = \frac{1}{N}\sum_{n=1}^{N}(w^Tx_n - y_n)^2$$

方便推导，写成矩阵形式

求出使$E_{in}(w)$最小的$w$，就是我们最终需要的解。

求解步骤

$E_{in}(w)$ continuous, differentiable and convex, close form solution exists.

问题是连续可导且凸，存在解析解，对$E_{in}(w)$求导，使导数为零，即可得到。将其展开，不难得到

$$\begin {align} E_{in}(w) &= \frac{1}{N}||Xw-y||^2 \\ &= \frac{1}{N}(Xw-y)^T(Xw-y) \\ &= \frac{1}{N}(w^TX^T-y^T)(Xw-y) \\ &= \frac{1}{N}(w^TX^TXw-2w^TX^Ty+y^Ty) \end {align}$$

因为向量內积满足交换律，不难得到$y^TXw = w^TX^Ty$。

对列向量$w$求导，求导过程中用到几个性质，将$w$展开很容易证明

• $\nabla_w(w^Tb) = b$
• $(w^TAw) = \sum \sum w_iw_jA_{ij}$
• $\nabla_w(w^TAw) = (A + A^T)w$

不难得到

$$\nabla E_{in}(w)=\frac{2}{N}(X^TXw - X^Ty)=0$$

得到ordinary least squares(OLS)解。

$$w_{lin} = (X^TX)^{-1}X^Ty$$

其中$X^+=(X^TX)^{-1}X^T$称为pseudo-inverse of X。算法汇总到一张Slide如下

算法Intuition

首先引入Hat Matrix的概念

$$\hat y=Xw_{lin}$$ $$\hat y=X(X^TX)^{-1}X^Ty$$

其中$H=X(X^TX)^{-1}X^T$叫做Hat Matrix。

The estimate $\hat y$ is a linear transformation of the actual $y$ through matrix multiplication with $H$.

根据Hat Matrix的表达式，很容易证明有如下性质

• $H^T=H$
• $H^K=H$
• $(I-H)^K=I-H$
• $trace(H)=d+1$
• $trace(I-H)=N-(d+1)$

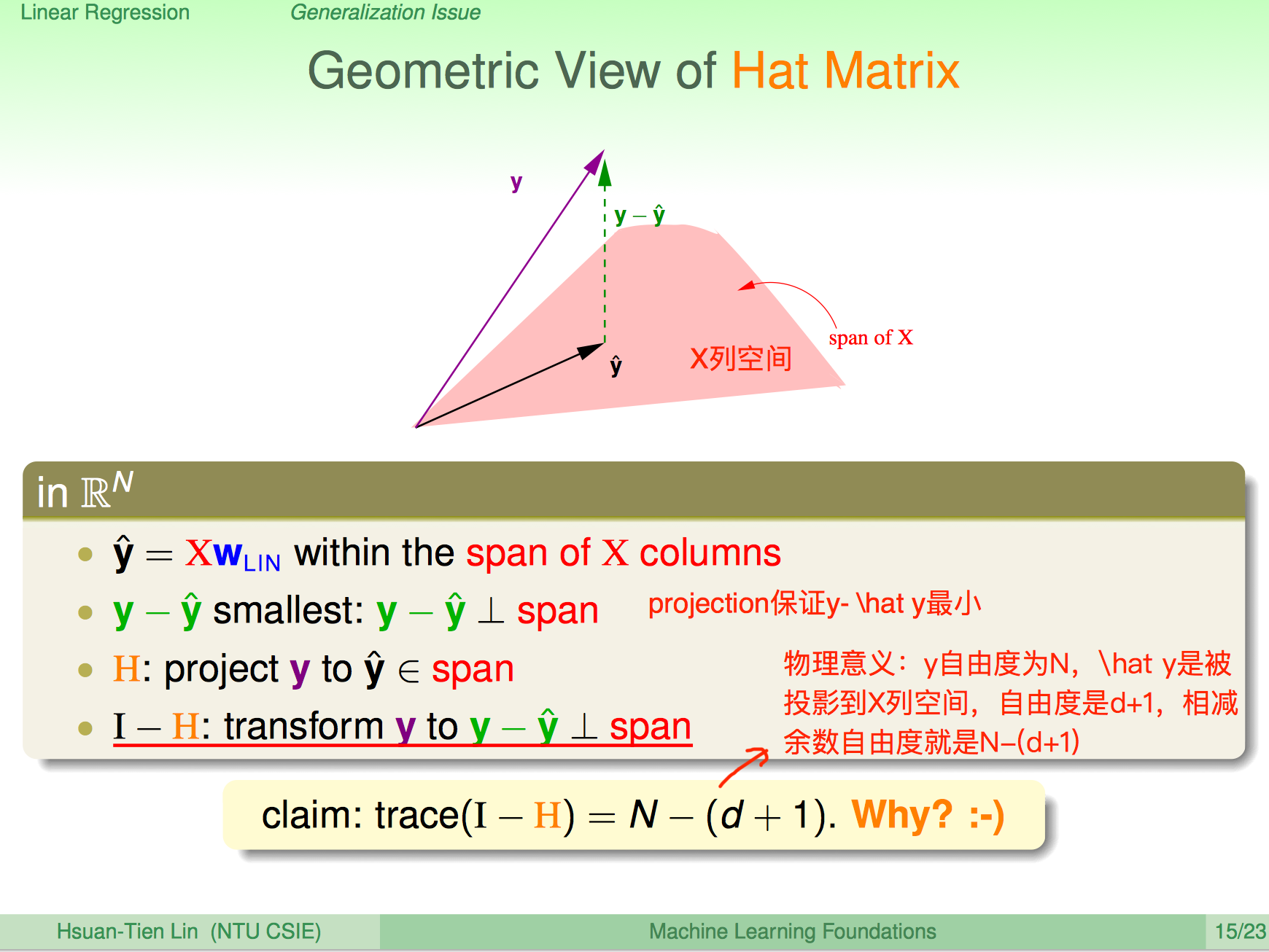
Hat Matrix直观几何意义就是将$y$投射到$X$的列空间。

误差推导

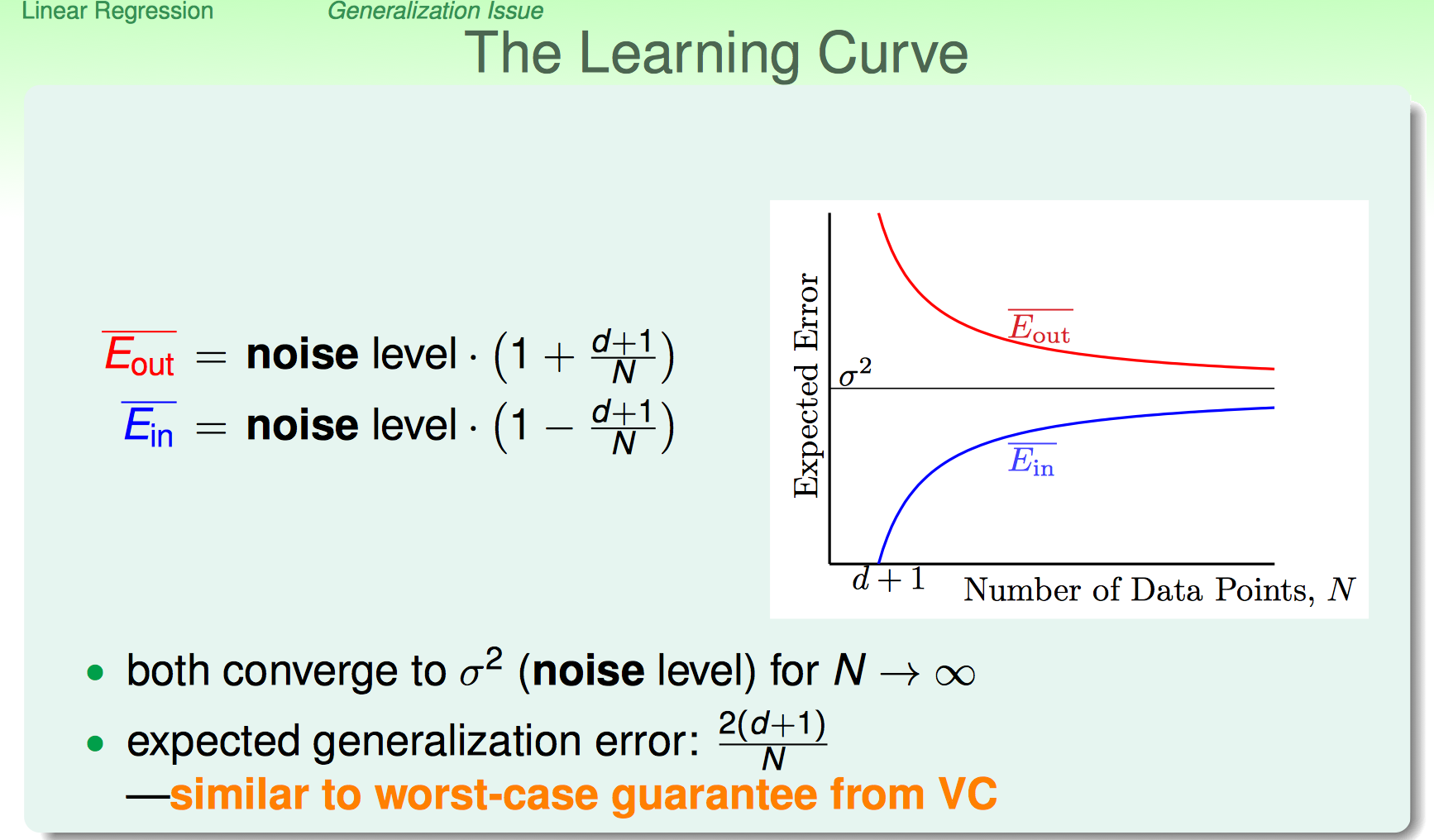
课程给出$\bar E_{in}(w)$比较直观的推导。

数学上简单证明

$$\bar E_D[E_{in}(w_{lin})] = \sigma^2(1-\frac{d+1}{N})$$

基本假设是线性函数加上噪音

$$y = Xw^* + \epsilon$$

代入下面式子

$$\begin {align} \hat y &= Hy \\ &=X(X^TX)^{-1}X^T(Xw^*+\epsilon) \\ &= Xw^* + H\epsilon \end {align}$$

然后再将$y$表达式反代回来

$$\hat y = y - \epsilon + H\epsilon$$

得到

$$\hat y - y = (H-I)\epsilon$$

所以

$$\begin{align} E_{in}(w_{lin}) &= \frac{1}{N} (\hat y - y)^T (\hat y - y) \\ &= \frac{1}{N} \epsilon^T (H-I)^T (H-I) \epsilon \\ &= \frac{1}{N} \epsilon^T (I-H) \epsilon \end{align}$$

对其求期望

$$\begin{align} \bar E_D [ E_{in}(w_{lin})] &= \frac{1}{N} \bar E_D[\epsilon^T (I-H) \epsilon] \\ &= \frac{1}{N} (\bar E_D[\epsilon^T \epsilon] - \bar E_D[\epsilon^T H \epsilon]) \\ &= \sigma^2 (1 - \frac{d+1}{N}) \end{align}$$

其中

$$\begin{align} \bar E_D[\epsilon^T \epsilon] &= \bar E_D[\epsilon_1^2 + \epsilon_2^2 + \dots + \epsilon_N^2] \\ &= \bar E_D[\epsilon_1^2] + \dots + \bar E_D[\epsilon_N^2] \\ &= N \sigma^2 \end{align}$$

以及

$$\begin{align} \bar E_D[\epsilon^TH\epsilon] &= \bar E_D[\sum_{i=1}^{N} H_{ii} \epsilon_i^2 + \sum_{i \neq j}^{N}H_{ij} \epsilon_i \epsilon_j] \\ &= \bar E_D[\sum_{i=1}^{N} H_{ii} \epsilon_i^2] + \bar E_D[\sum_{i \neq j}^{N}H_{ij} \epsilon_i \epsilon_j] \\ &= trace(H) \sigma^2 + 0 \\ &= \sigma^2 (d+1) \end{align}$$

$\epsilon_i$和$\epsilon_j$相互独立，且其期望都为0。

最终的到Learning Curve如下