多分类模型
分类是常见的机器学习任务,本文简单介绍分类的几种经典形式,即二分类、多分类和多标签分类。
常见分类任务
常见分类任务有以下三种
- 二分类「比如是否点击」
- 多分类「类别之间互斥,比如动物是猫、是狗还是老鼠」
- 多标签分类「不互斥,如文章主题可以同时是宗教、政治」
二分类相对直接,比如常见的Logistic Regression。本文着重梳理多分类和多标签学习。
多分类
多分类「类别之间互斥」可通过三种方式实现,可直接通过多分类模型,也可通过二分类模型:
- 直接运用多分类模型,如Softmax Regression
- One Versus All
- One Versus One
假设样本类别有$y \in {1,2, \dots, K}$。
多分类模型
直接学习多分类模型,比如常见的Softmax Regression,模型输出在$K$个类上的概率分布,概率最大的即为预测类别。
One-Versus-All
又叫One-Versus-Rest,学习$K$个二分类器「可并行」,取这个$K$个二分类器中概率最高的那个为作为预测类别。参考吴恩达和林轩田两位老师的图示
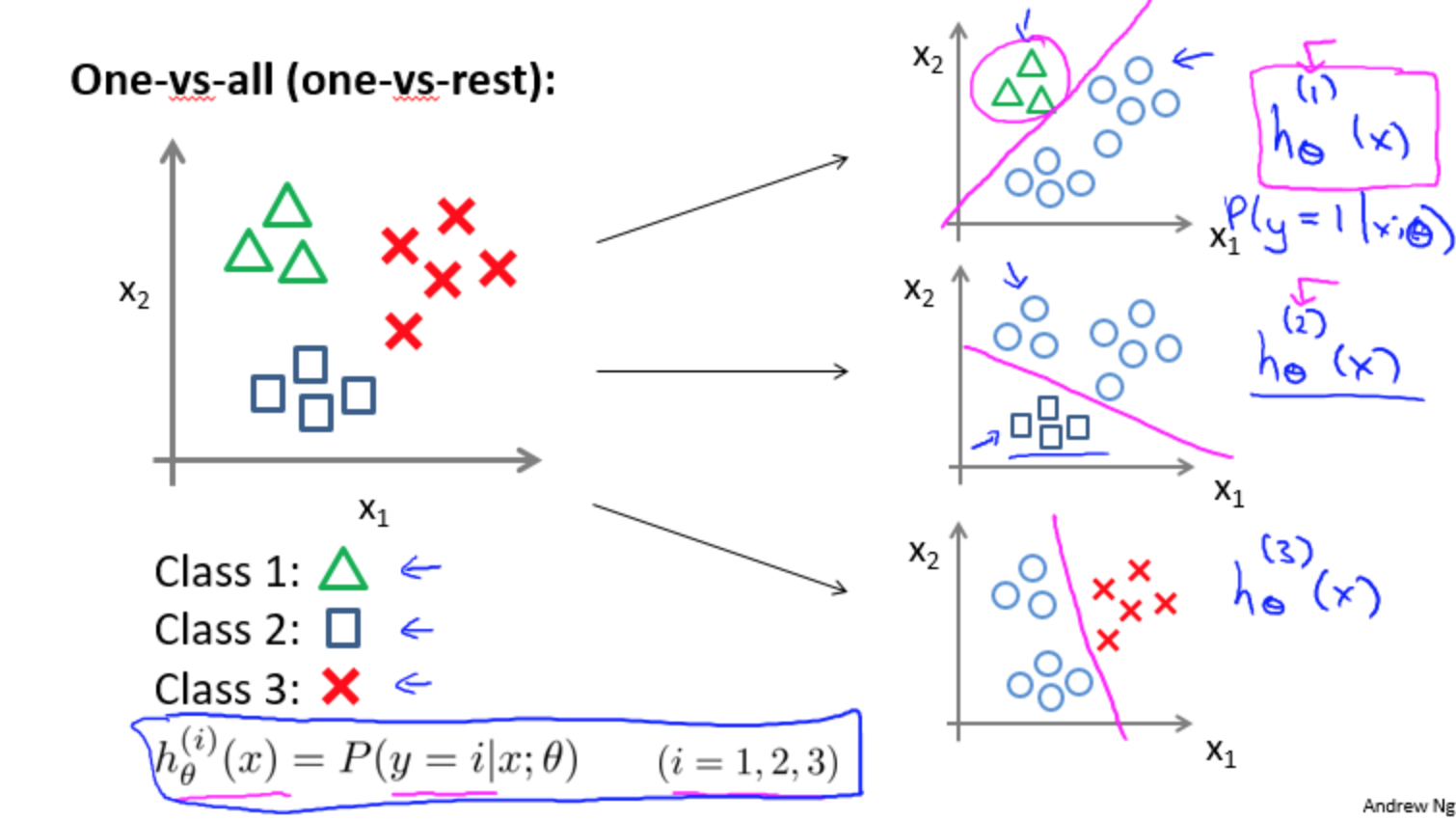
二分类器$1$输出$P(y=1\vert x)$的概率;二分类器$2$输出$P(y=2\vert x)$的概率;二分类器$K$输出$P(y=K\vert x)$的概率。选择这$K$个分类器中置信度最大的作为最终预测。

One-Versus-Rest潜在的问题是,如果$K$比较大,样本很可能不均衡。
One-Versus-One
学习$K(K-1)/2$个分类器,取这些分类器分类结果的投票结果作为预测类别,参见林轩田老师「机器学习基石」课程Slide。

多标签分类
多标签问题比二分类和多分类都要棘手。因为样本类别不确定,有的样本只有一个类别,有的有多个类别;且类别之间可能存在相关性;多标签训练数据相对难获取。
一般有两种处理思路,一种是问题转化
Problem transformation methods: This category of algorithms tackle multi-label learning problem by transforming it into other well-established learning scenarios. Like Binary Relevance, Classifier Chains, Label Powerset.
另一种是改编算法
Algorithm adaptation methods: This category of algorithms tackle multi-label learning problem by adapting popular learning techniques to deal with multi-label data directly. Like Multi-Label k-Nearest Neighbor(ML-kNN), Multi-Label Decision Tree(ML-DT).
简要梳理下基于问题转化的思路,即二元关联「Binary Relevance」、分类器链「Classifier Chains」以及标签Powerset「Label Powerset」。
Binary Relevance
二元关联思路很直接,如果有$L$个标签,就训练$L$个二分类器,每个二分类器对应label space一个label。不难看出,其实二元关联没有考虑标签之间的相关性。
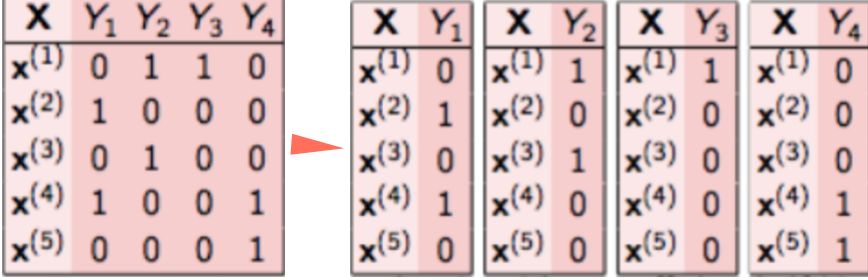
Classifier Chains
分类器链和二元关联思路类似,也是训练$L$个二分类器,区别是为了考虑标签的相关性,每个分类器的输入空间是不同的。如下图,黄色是输入空间,白色是输出空间。

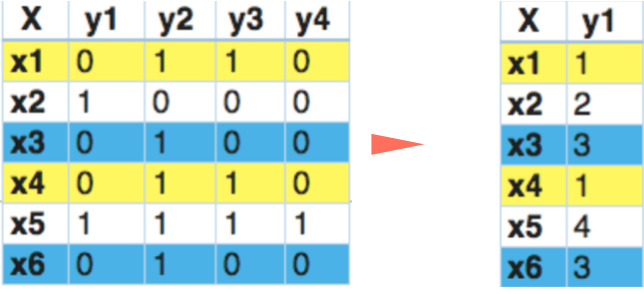
Label Powerset
标签Powerset将其转化为多分类问题。将训练数据中唯一的标签组合当做唯一标签,重新编码,这样就转化为多分类问题。如下图$x_1$和$x_4$的标签组合是一致的,重新编码为$1$,类似的有$x_2$与$x_5$,以及$x_3$与$x_6$。组合后标签数量随$L$成指数趋势增加,所以当$L$较大时,会产生数据稀疏问题。