06 Theory of Generalization

如果有Break Point，$m_H(N)$上限如何进一步简化，见详细课件。

脉络回顾

回顾之前一步步推演脉络。

• Bin of Marbles从$\nu$估算$\mu$，引入概率
• 引入Hoeffding不等式，理论上保证坏事情概率有上界
• 用一个假设，类比Bin of Marbles例子，某特定假设可学习
• 算法$A$从假设中选，引入Union Bound，Hoeffding不等式引入$M$
• Union Bound太loose，引入数据集Dichotomy，$M$替换为$2^N$
• $2^N$依然很大，引入Growth Function $m_H(N)$，进一步精确
• 引入Break Point，找到$m_H(N)$的上界，且摆脱对数据依赖
• $N^{k-1}$使有效假设数量降到多项式级(如果break point非无穷大)
• 证明$m_H(N)$可以替换$M$，泛化问题得证
• 学习是可行的！

Bounding Function

如果存在break point，可以找到growth function上界，从而摆脱对特定数据集的依赖，且不用给出其具体表达式。

$m_H(N)$ is $poly(N)$ if break point exists.

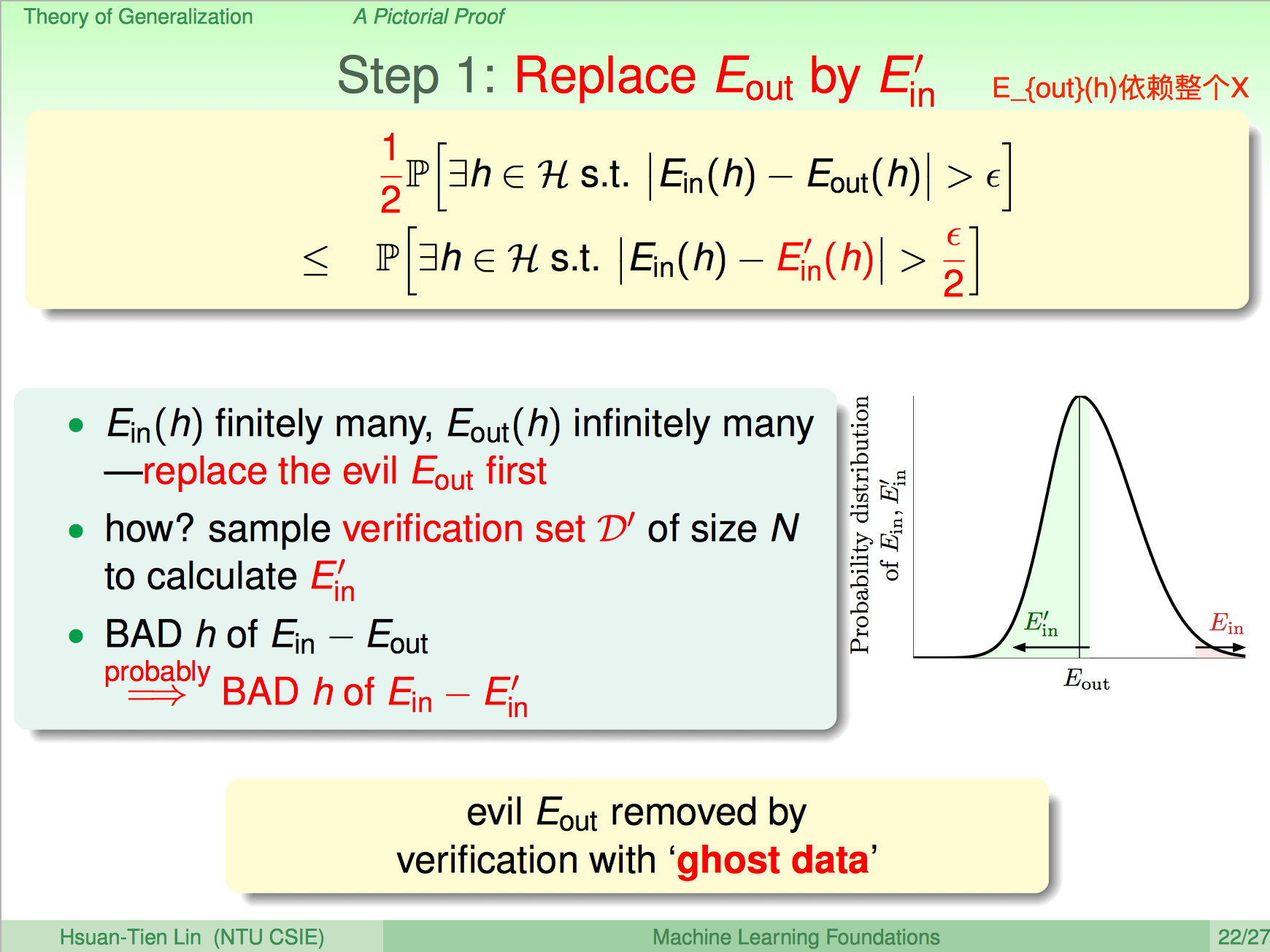
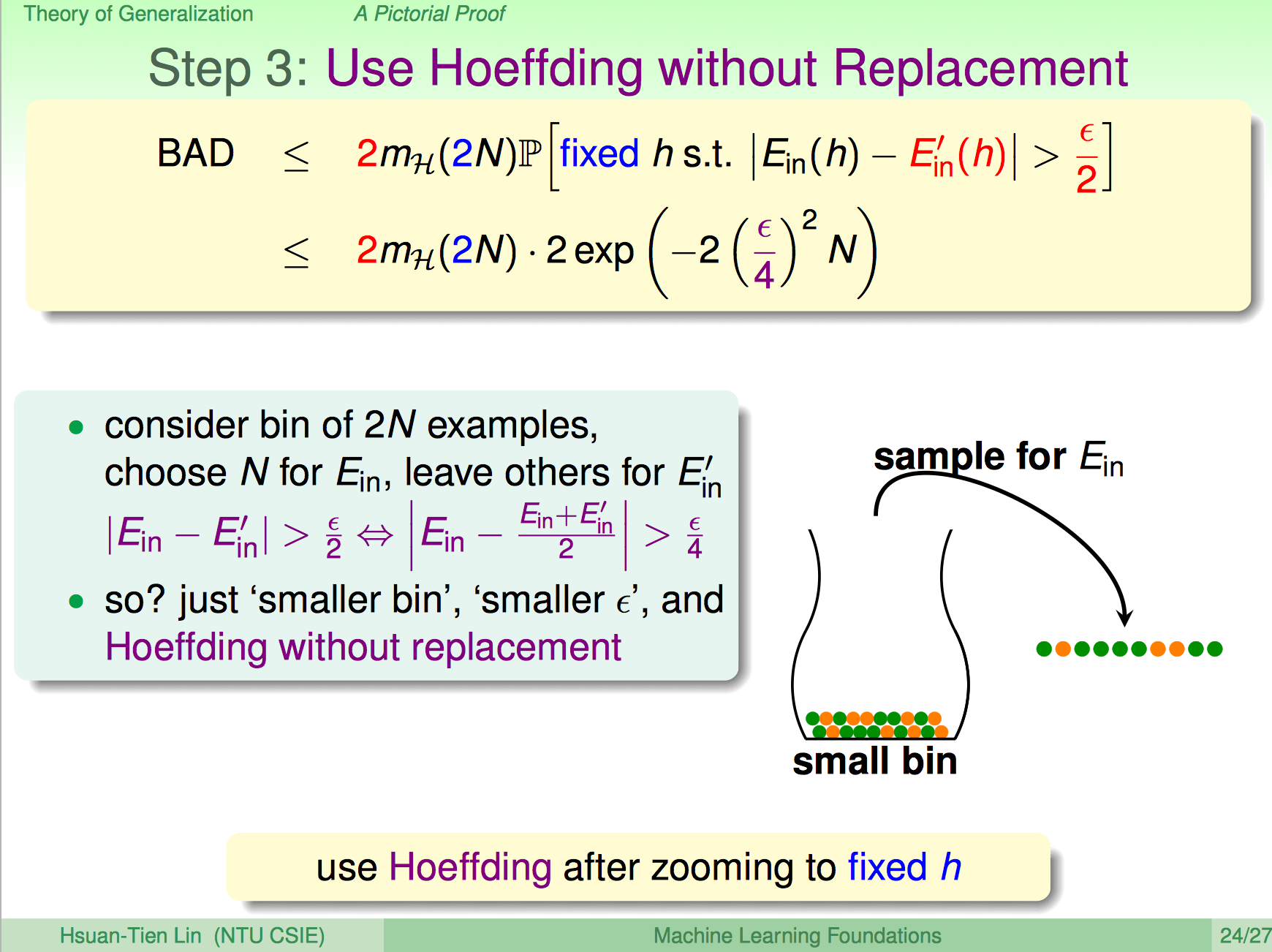
A Pictorial Proof

Theory of Generalization最后的证明：

如何用$m_H(N)$替换上式中的$M$，完成理论的最后一跃？