07 The VC Dimension

详细介绍VC维的概念，见详细课件。

VC Dimension

VC dimension of $H$, denoted $d_{VC}(H)$ is largest $N$ for which $m_H(N)=2^N$.

也就是假设空间$H$能shatter的最大样本量$N$。

一般地：

If $N\ge2,d_{VC}\ge2, m_H(N) \le N^{d_{VC}}$

VC维给growth function一个更简洁的上界。只要不是$d_{VC} \ne \infty$，就能保证$g$泛化s，即$E_{out}(g) \approx E_{in}(g)$，VC维给出worst case guarantee on generalization。

VC Dimension of Perceptrons

感知机的VC维：

d-D perceptrons: $d_{VC} = d + 1$.

证明分两步，首先证明：

$d_{VC} \ge d + 1$ => There are some $d + 1$ inputs we can shatter.

只要保证$X$矩阵可逆，对任意$y$均可找到对应的$w$，也就是可以shatter这个规模数据集。

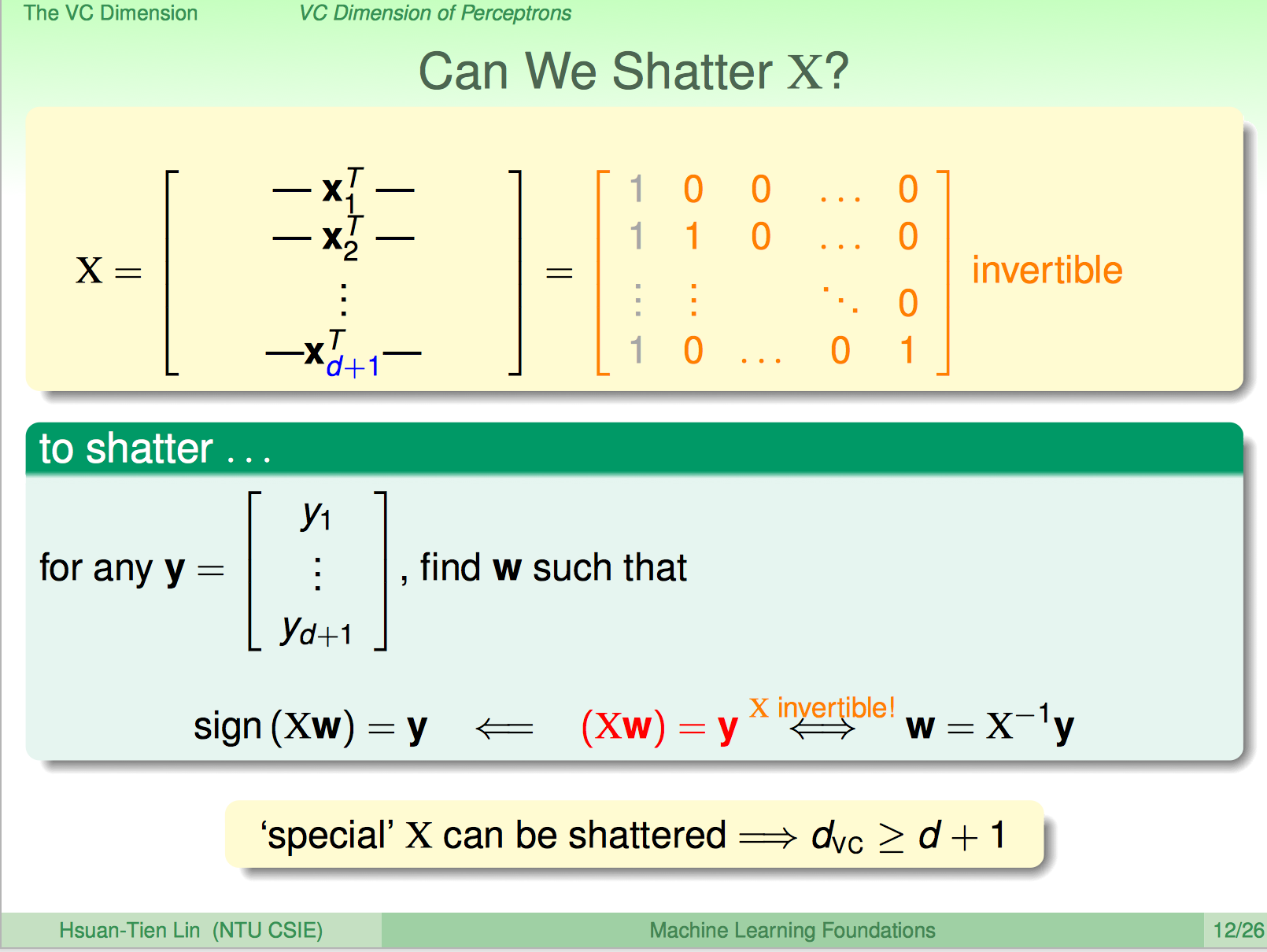
其次证明：

$d_{VC} \le d + 1$ => We cannot shatter any set of $d + 2$ inputs.

$d+2$个$d+1$维向量，必然线性相关，对任意$X$，图中所说的case都不能shatter，所以上界得证。

Intuition

$d_{VC}(H)$可以理解为模型的自由度，可衡量模型的capacity。

Practical rule of thumb: $d_{VC}$ approximates number of free parameters(but not always).

Perceptrons有$d+1$个有效参数，其VC维就是$d+1$。

Interpreting VC Dimension

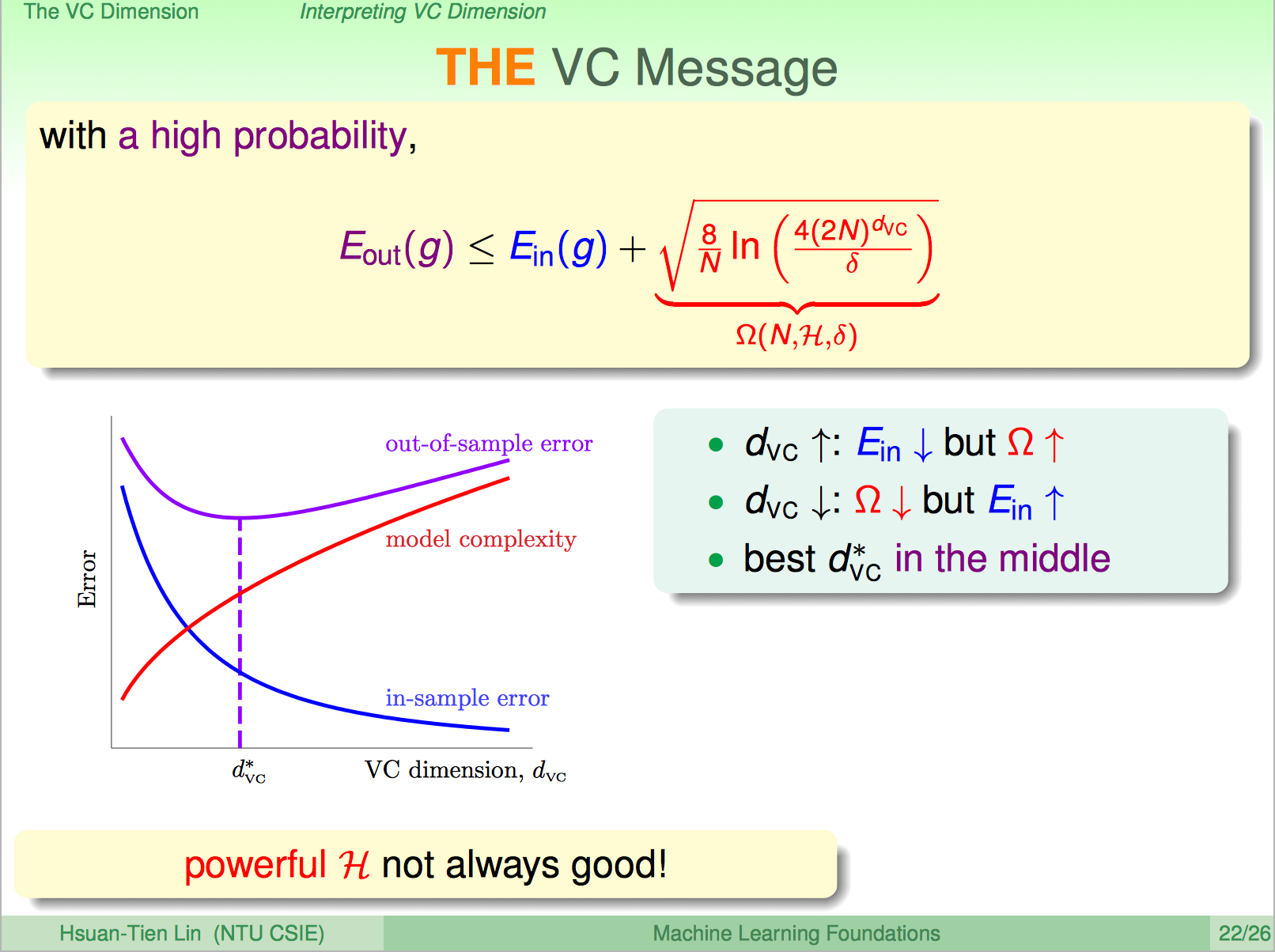
重新表述VC Bound，可以这样说，有很大概率，模型的泛化误差在某个边界内。

可以看到VC维如何影响模型的样本外误差。

一般情况下，样本数据量取10倍VC维大小，能至少保证不错的学习效果。