08 Noise and Error

在target function有noise的时候，VC bound holds；介绍最基本的错误衡量方式，见详细课件。

Noise

理想情况下，存在一个target function，但噪音总会存在，比如信用卡审批例子

• noise in $y$, good customer, mislabeled as bad
• noise in $y$, same customers, different labels
• noise in $x$: inaccurate customer information

关心的问题是，如果存在Noise，VC bound是否依然成立？

考虑推导用最原始的Bin of Marbles的例子，如果i.i.d.，后面一系列推导假设类似，即VC bound holds。

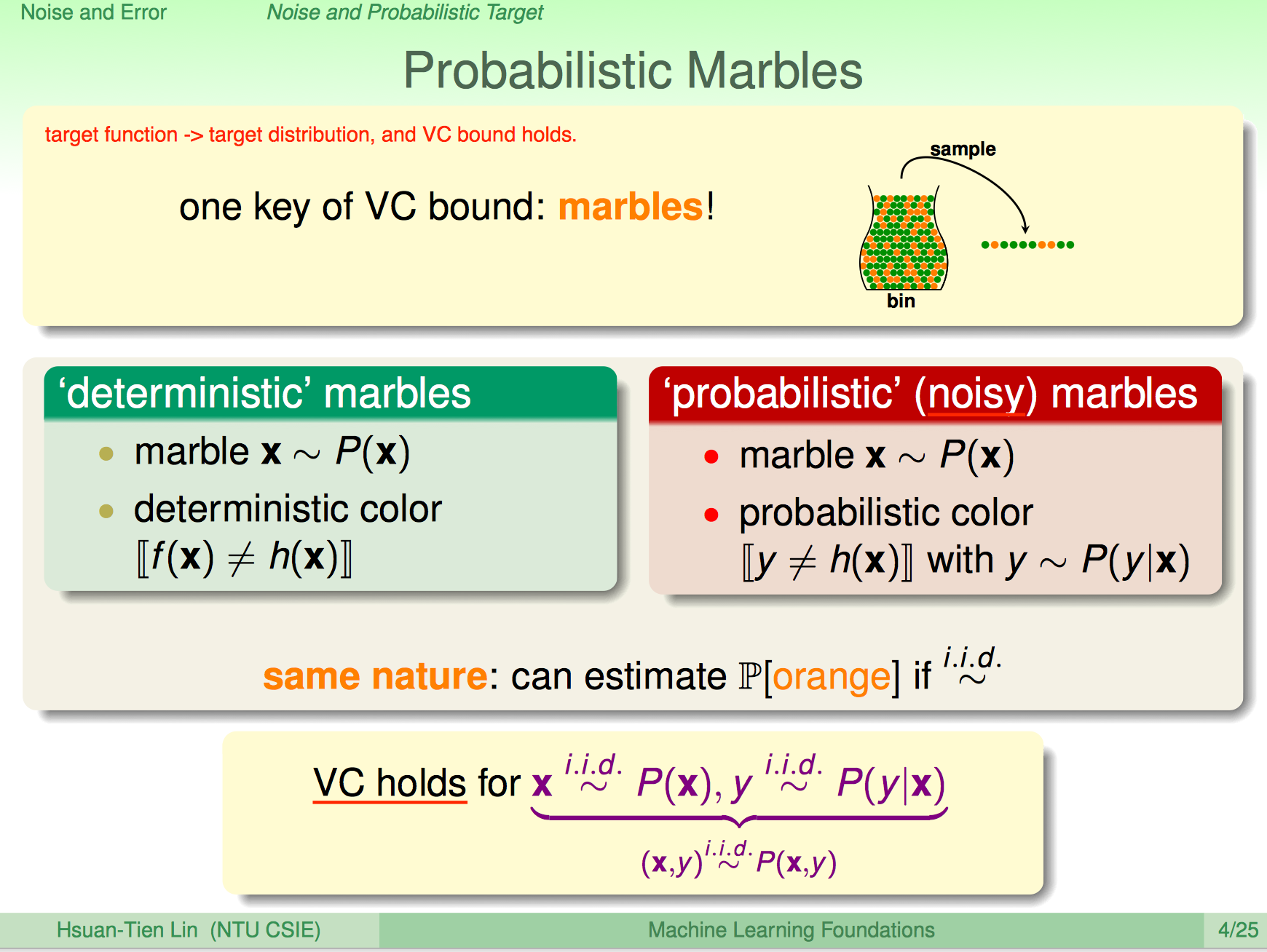
关于target distribution，其实可以看做

ideal mini-target + noise

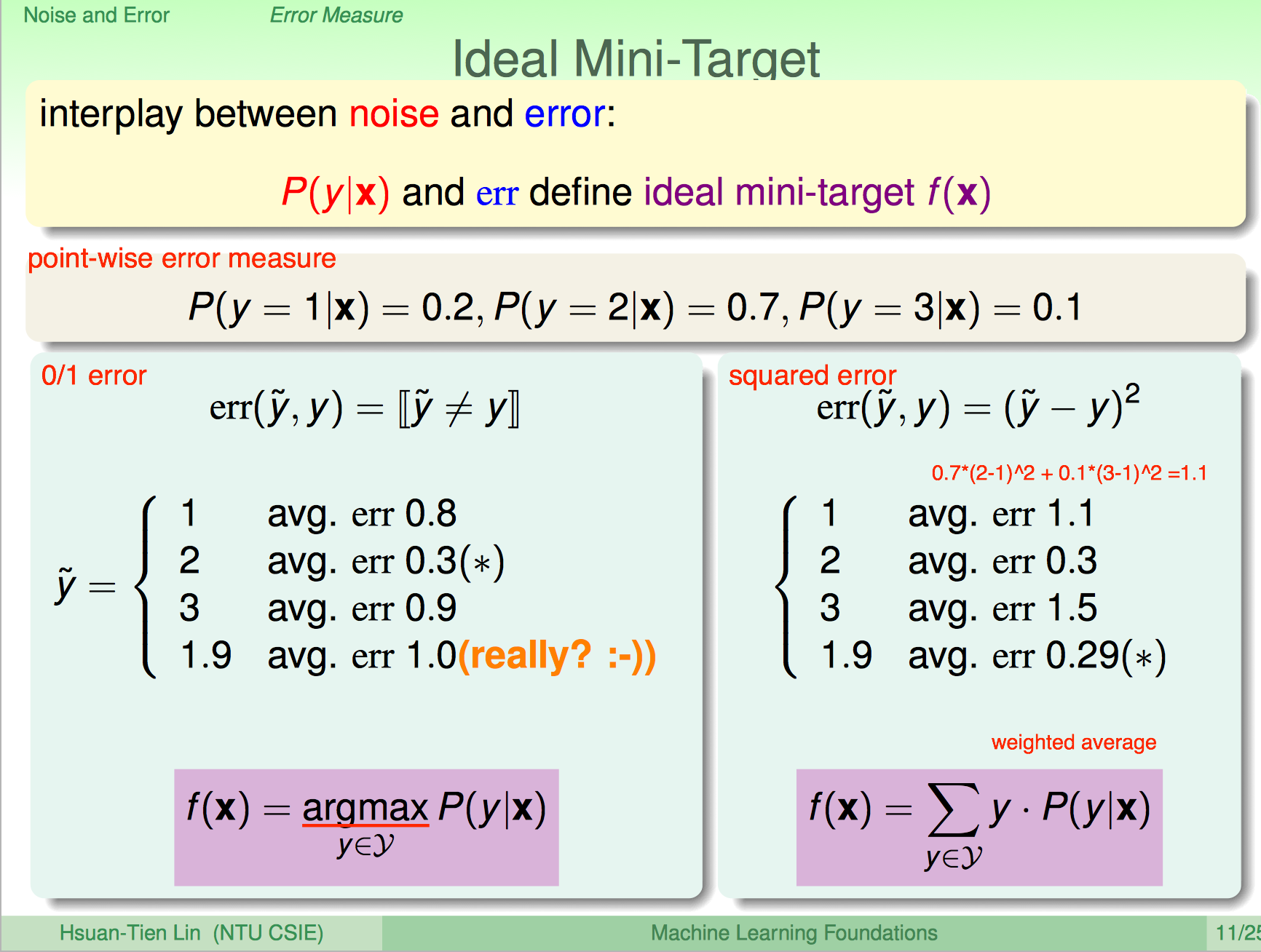
Error Measure

用以衡量$g$于$f$的相似程度。常见的比如point wise error measure，不同学习任务，对应的error measure也不一样。

Algorithmic Error Measure

Error measure一般要根据学习任务设定。

err is application/user-dependent

比如0/1 error penalizes both types equally，但有些场景是不太适用的，比如Fingerprint Verification for Supermarket/CIA。

对超市来说，false accept代价很小，false reject代价稍大。

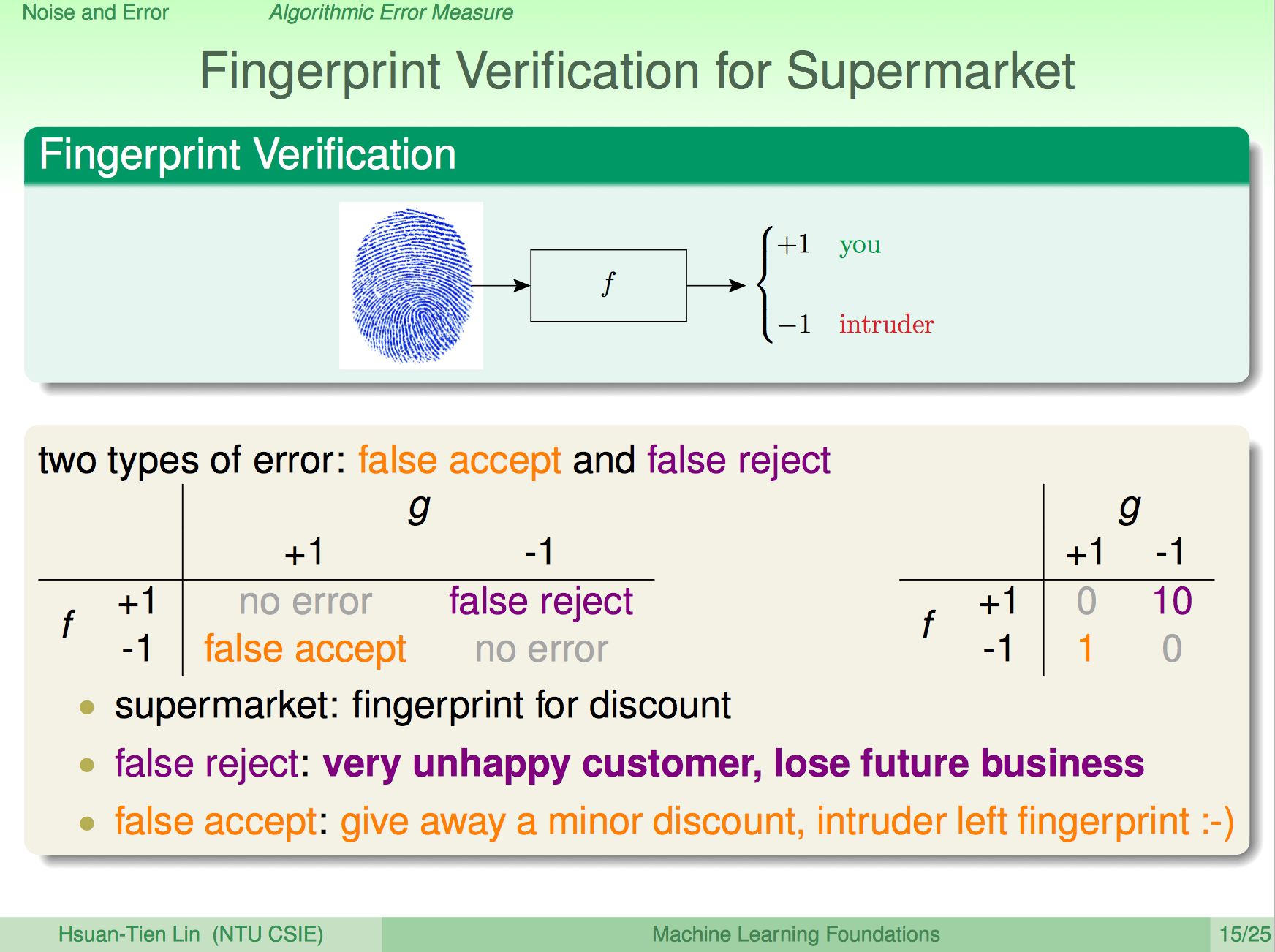
对CIA来说，false accept代价极大，false reject代价不大。

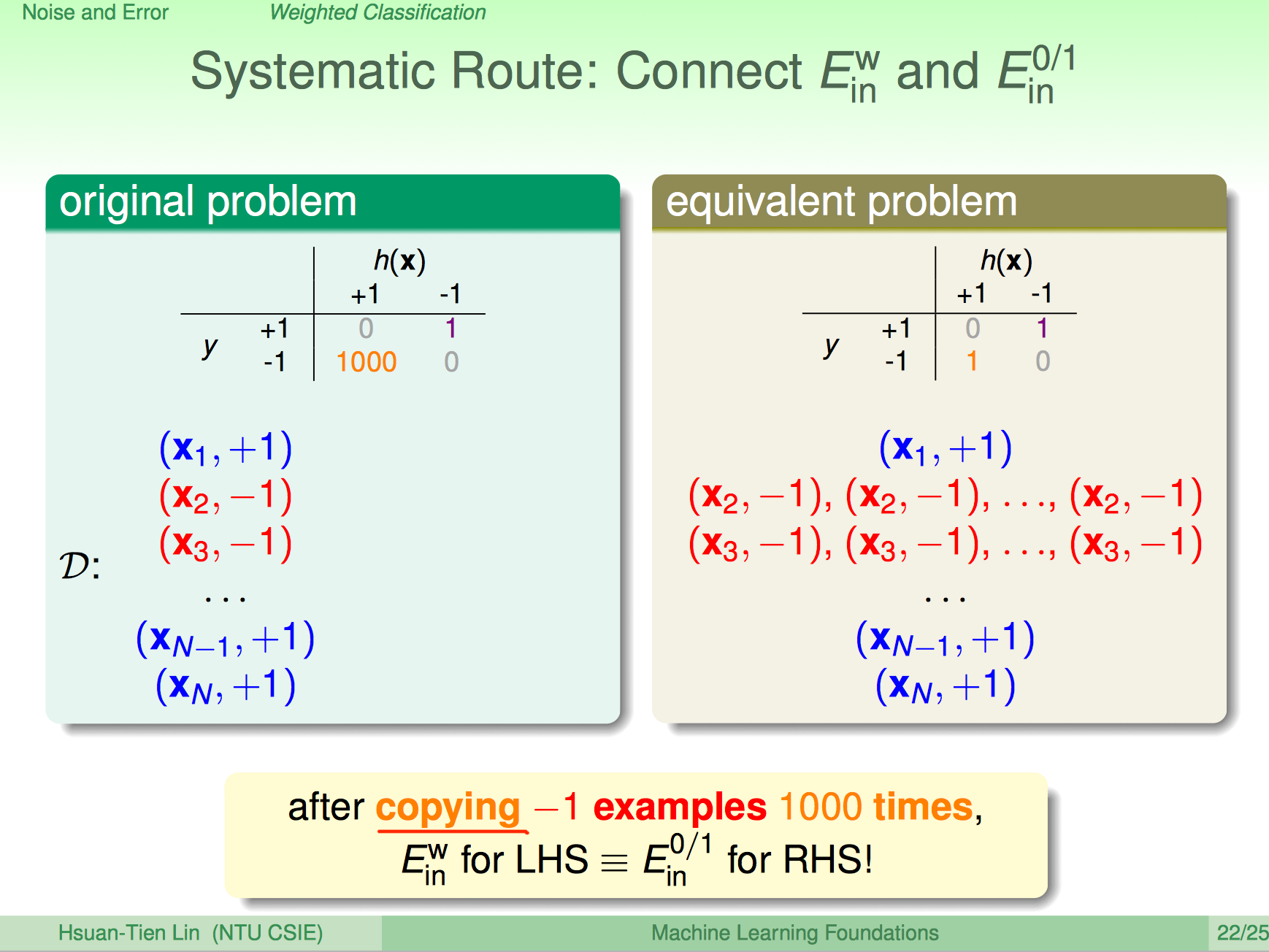
Weighted Classification

不同的误分类代价不同，权重不同，error measure也不一样，算法能保证$E_{in}^w(h)$较小吗？

其实算法能保证$E_{in}^{0/1}$较小，$E_{in}^{w}$只需要把权重大的样本多访问几次，就得到等价问题。