XGBoost原理简介
XGBoost是经典的提升树学习框架,其配套论文和PPT分享也相当经典,本文简单梳理其思路,以备忘。
整体思路
和一般提升模型一样,提升树模型也遵循相同的范式
- 采用加法模型「forward stage-wise manner」
- 每轮引入一weak learner「此处是一棵CART树」
- 学习之前weak learners的不足「用梯度表征」
同时要考虑过拟合等问题「overfitting is everywhere」。
Tree Ensemble
遵循李航老师统计学习三要素公式
假设空间「模型」
Tree Ensemble基本思想是将多棵树的结果融合作为最终输出,示意图如下
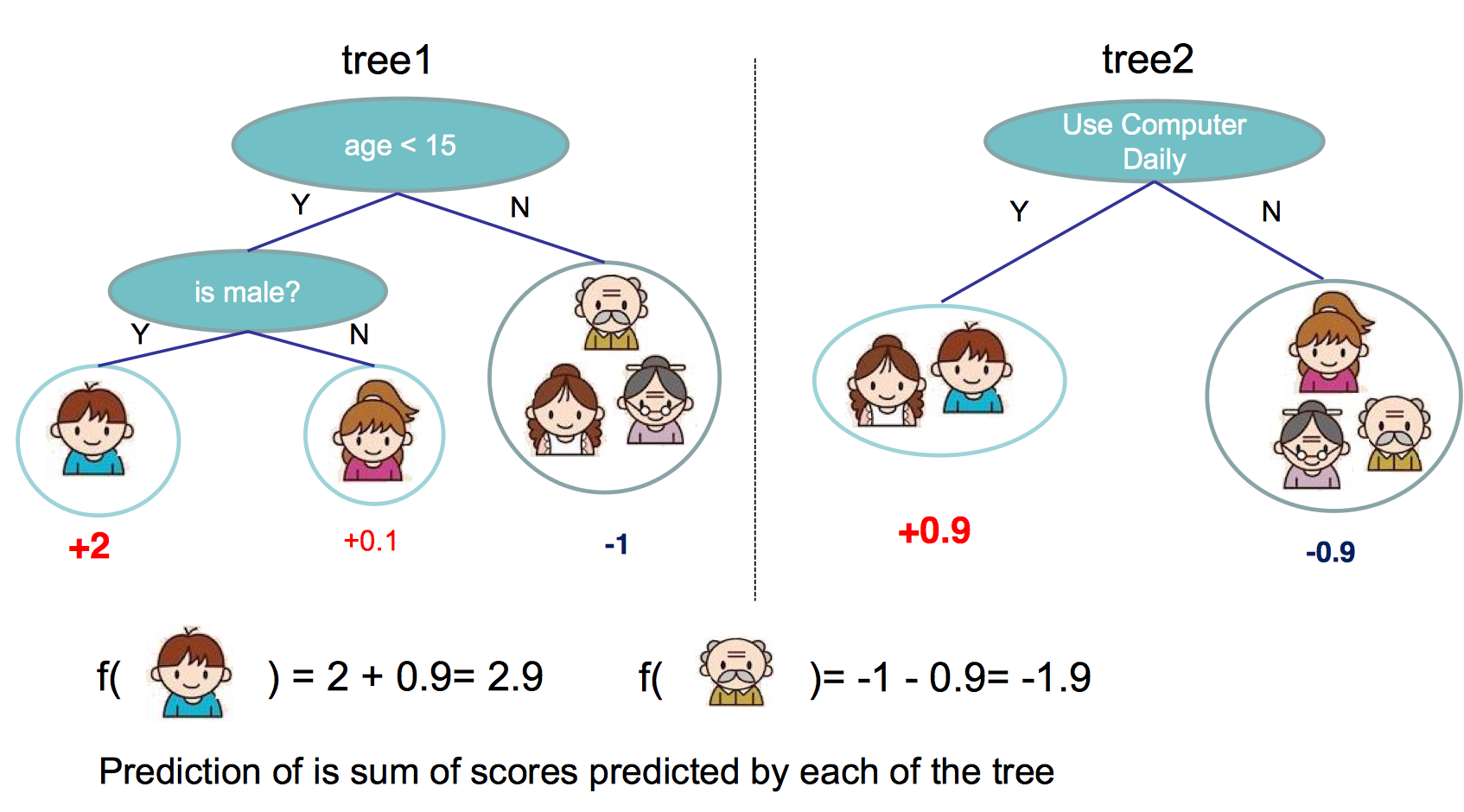
不难看出,模型的假设空间是一系列CART树的集成,输出为
其模型参数为$K$颗树
目标函数「策略」
模型假设有了,另一个核心元素就是目标函数,和一般监督模型一样
目标函数分两部分「Bias-variance tradeoff is everywhere」
- Training Loss measures how well model fit on training data
- Regularization measures complexity of model
具体到Tree Ensemble,其目标函数为
优化求解「算法」
模型参数的最终求解。参数$\circleddash = {f_1, f_2, \dots, f_K}$为$K$颗树,无法用SGD类似方法优化求解,因为不是$R^d$空间上的数值向量。一般采用Additive Training(Boosting)的思想求解。
Gradient Boosting
Tree Ensemble章节回答了what we are learning的问题,Gradient Boosting章节要回答how do we learn的问题。
Additive Traing范式
采用Additive Training(Boosting)的模式,即每一轮学习一颗新树$f_t$

学习一颗新树
问题是每一轮$\hat y_i^{(t)} = \hat y_i^{(t-1)} + f_t(x_i)$中,$f_t$如何学习?
Define objective(loss, regularization) and optimize it.
在第$t$轮,树的每一次生长,确定选那个特征分裂/分裂点取在哪里即可。其依据是使Objective最小,这里涉及两点,即$w\in R^T$取何值Objective最小,以及Objective最小值表达式是什么。
定义Objective及其近似
Objective是$w$的一般函数,其最小值一般表达式并不完全确定「not general」。XGBoost对其进行二阶泰勒展开近似,推导变换后Objective可形式化为$T$个独立的二项式,表达式可统一「只需Objective一阶二阶可导即可」。
以下简单梳理推导核心步骤。

其中每次迭代$f_t(x)$视为$\Delta x$泰勒近似展开,用一阶二阶导表示。对应到Square Loss后理解会更直观一些,一阶导正比于残差,二阶导为常数。
经过简化,现在Objective为
此时学习只依赖loss function一阶二阶导,理论理解和工程实现都简洁不少。
The learning of function only depend on the objective via $g_i$ and $h_i$.
确定Objective最小值
为方便推导,需要一些符号表示上的辅助
- 变换树的表达方式,见下文「如何表征一棵树」章节
- $I_j$表示落在第$j$个叶子节点所有样本集合
- 详细符号含义见下文「符号约定」章节
- 「正则项」考虑叶子节点数以及叶子分的L2范数,见下图
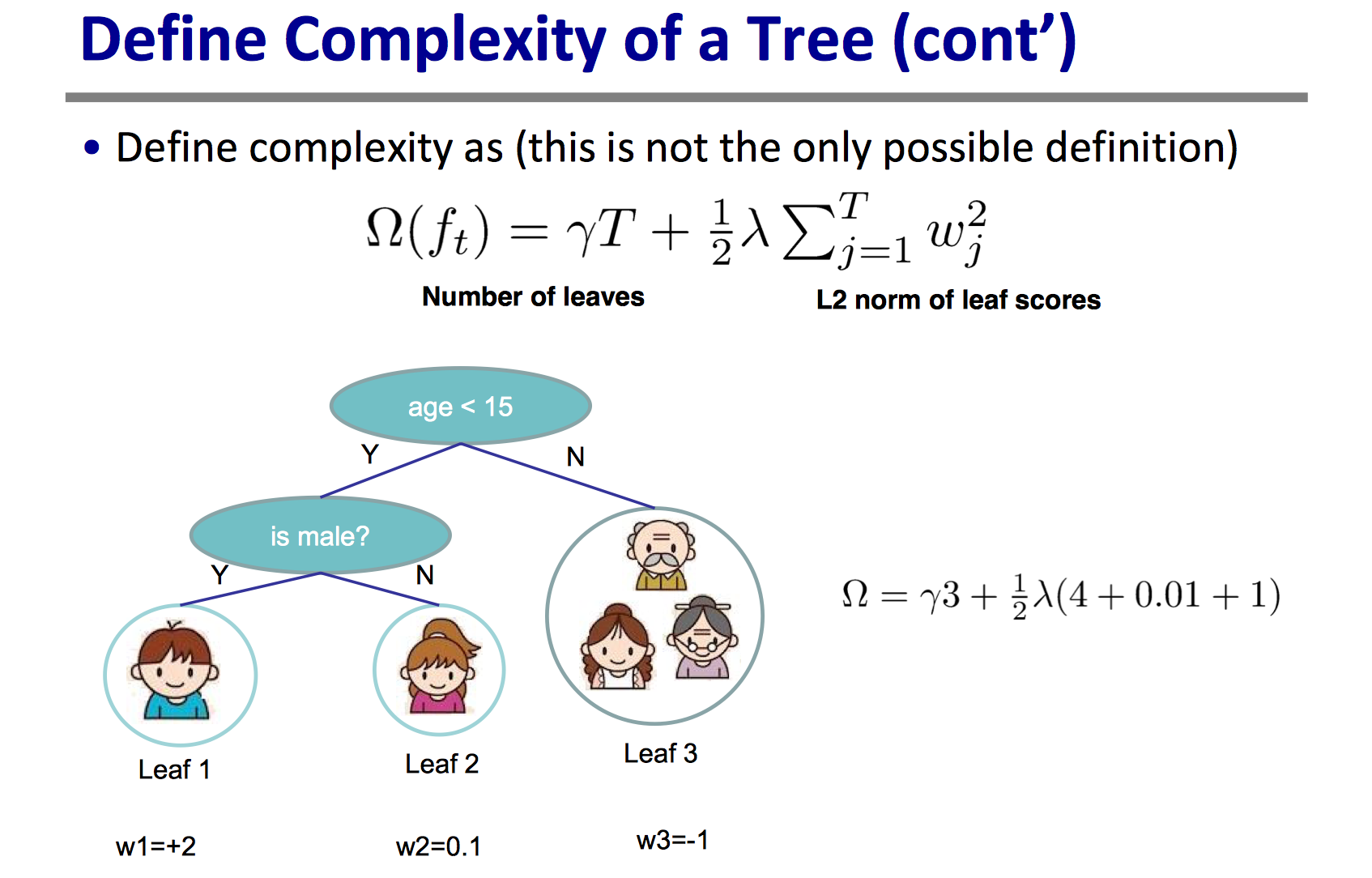
不难推导如下式子
对上述四个式子几点解释
- 式子1是经过泰勒展开近似的目标函数
- 式子2考虑树新表达方式,公式加入正则项
- 式子3将$n$个样本,按划分的叶子节点重新group,整合train loss和regularization
- 式子4引入$G_j$和$H_j$简化表达
- 式子4是$T$个独立的二项式
对二项式$y = ax^2 + bx + c$,在$x=-\frac{b}{2a}$取极值$y=\frac{4ac-b^2}{4a}$。不难得出$w^*$取值为
时,Obj有以下最小值
最小值中包含两项,第一项表示树拟合好坏,第二项表示树的复杂度。如此,即可根据gain选择分裂特征和分裂点了。
一点验证
当模型为GBDT,Loss选为Square Loss,不加正则项,其结论应该跟上述推导完全一致。Square Loss
求一阶导
即其一阶导是负残差。求二阶导,其值为常数
Square Loss情况下,取$I_j$集合的均值「残差均值」作为该节点预测值「optimal weight」,应该跟$w^*$保持一致。
不难看出
- $\lambda=0$ 此处无正则
- $H_j = \vert I_j\vert$ 为$I_j$样本个数
- $G_j$ 残差之和
综上,其optimal weight即为残差均值,其实是XGBoost里$w_j^*$的特例。
如何表征一棵树
决策树可看做一系列If-Then规则的集合,但这样表示起来比较麻烦。为了方便公式的推导,XGBoost将其表示为一向量。
Think regression tree as a function that maps the attributes to the score. We define tree by a vector of scores in leafs, and a leaf index mapping function that maps an instance to a leaf.
即用长度为$T$「叶子节点数」的向量$w$和将样本实例映射到叶子索引的映射函数$q(x)$表示。
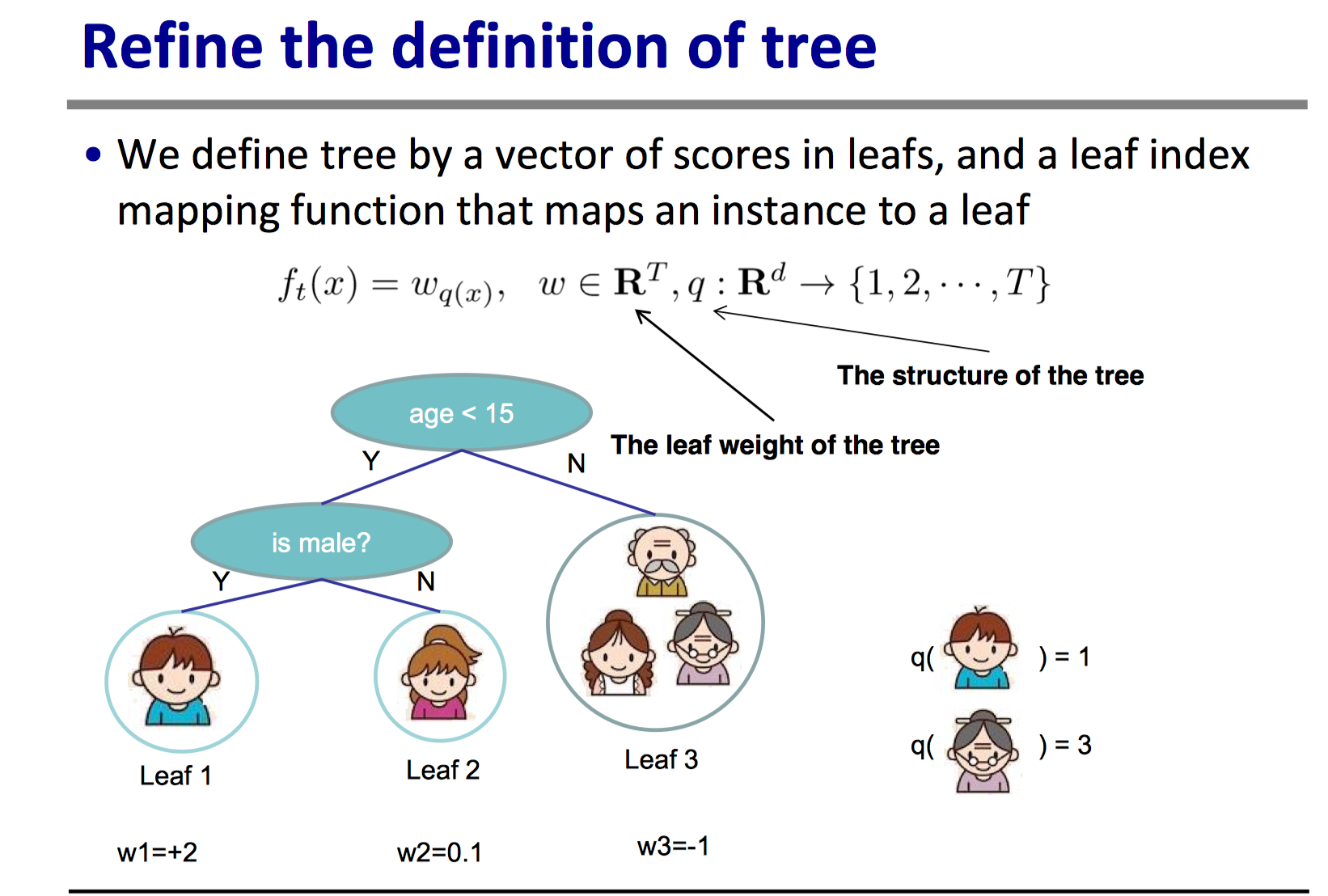
这样树的预测输出可直接用$w$表示,跟正则项$\vert w\vert ^2$保持一致,公式表示推导上比较方便。
如何防止过拟合
XGBoost中有很多防止过拟合手段,比如
正则化
每一轮树的目标函数Objective中可以包含正则项,是防止过拟合经典手段
Shrinkage
每一轮树都不完全拟合残差或梯度,给后续学习器学习的空间
$\epsilon$ is called step-size or shrinkage, usually set around 0.1. This means we do not do full optimization in each step and reserve chance for future rounds, it helps prevent overfitting
Column Subsampling
随机森林里使用的经典方法,也叫做feature subsampling,每次只用一部分特征学习,也可防止过拟合。
Candidate Proposal
在选择连续特征分裂点时,不遍历所有可能值「exact greedy algorithm」,而是由数据分位点生成一系列候选「candidate proposal」,从中选择分裂点。这样不仅降低了计算量,同时还有一定防止过拟合效果。
特征重要性
树模型一个优点就是可以确定特征重要性,具体如何做呢?XGBoost里提供这几个衡量标准
- 该特征作为分裂特征在所有树中出现的次数
- 该特征作为分裂特征的增益「avg&total」
- 该特征作为分裂特征的对样本的覆盖「avg&total」
详细可参考文档Python API Reference。
当然还有更一般化确定特征重要性的方法,比如Permutation Test,林轩田老师在机器学习技法中随机森林章节中有介绍。其基本思想是某一维特征做permutation,依据模型performance的下降程度判定特征重要性。
符号约定
- $(x_i, y_i)$ 表示样本输入
- $\hat y_i$ 表示模型在$x_i$上的输出
- $f_t(x)$ 表示第$t$论学习的树
- $l(y_i, \hat y_i)$ 表示Training Loss
- $\Omega(f_t)$ 表示树$f_t$的复杂度,正则项
- $q(x_i)$ 表示$x_i$对应的叶子节点索引
- $w$ 表示树叶子节点对应的得分向量
- $T$ 表示树叶子节点数
- $I_j={i\vert q(x_i)=j}$ 表示落到$jth$节点上样本集
- $G_j$ 表示$I_j$集合一阶导之和
- $H_j$ 表示$I_j$集合二阶导之和
