word2vec详解

关于word2vec的原理的一些理解。

Motivation

word2vec技术的motivation是设法学习词语的向量表示，使该向量能表达其含义，且在该向量空间中，相似的词语距离较近。在传统的One Hot表达方式下，所有词语的向量都正交，没有相似的概念。

Intuition

那到底该如何表达一个词语的含义呢？核心intuition是

You shall know a word by the company it keeps. (J. R. Firth 1957: 11)

A word’s meaning is given by the words that frequently appear close-by. 即通过与某词经常一起出现的词（上下文）确定其含义。

Modeling

那如何用数学方法建模上述想法呢？Christopher Manning在课程CS224N中总结其思路如下：

1. We have a large corpus of text
2. Every word in a fixed vocabulary is represented by a vector
3. Go through each position $t$ in the text, which has a center word $c$ and context (“outside”) words $o$
4. Use the similarity of the word vectors for $c$ and $o$ to calculate the probability of $o$ given $c$ (or vice versa)
5. Keep adjusting the word vectors to maximize this probability

根据上述思路，可以看出至少有以下问题需要解决。

样本构造

Go through each position $t$ in the text, which has a center word $c$ and context (“outside”) words $o$.

如何构造训练样本(center word, outside word)？以The Skip-Gram Model为例，每个中心词与其近邻词「window size内」组成训练样本，如下图所示

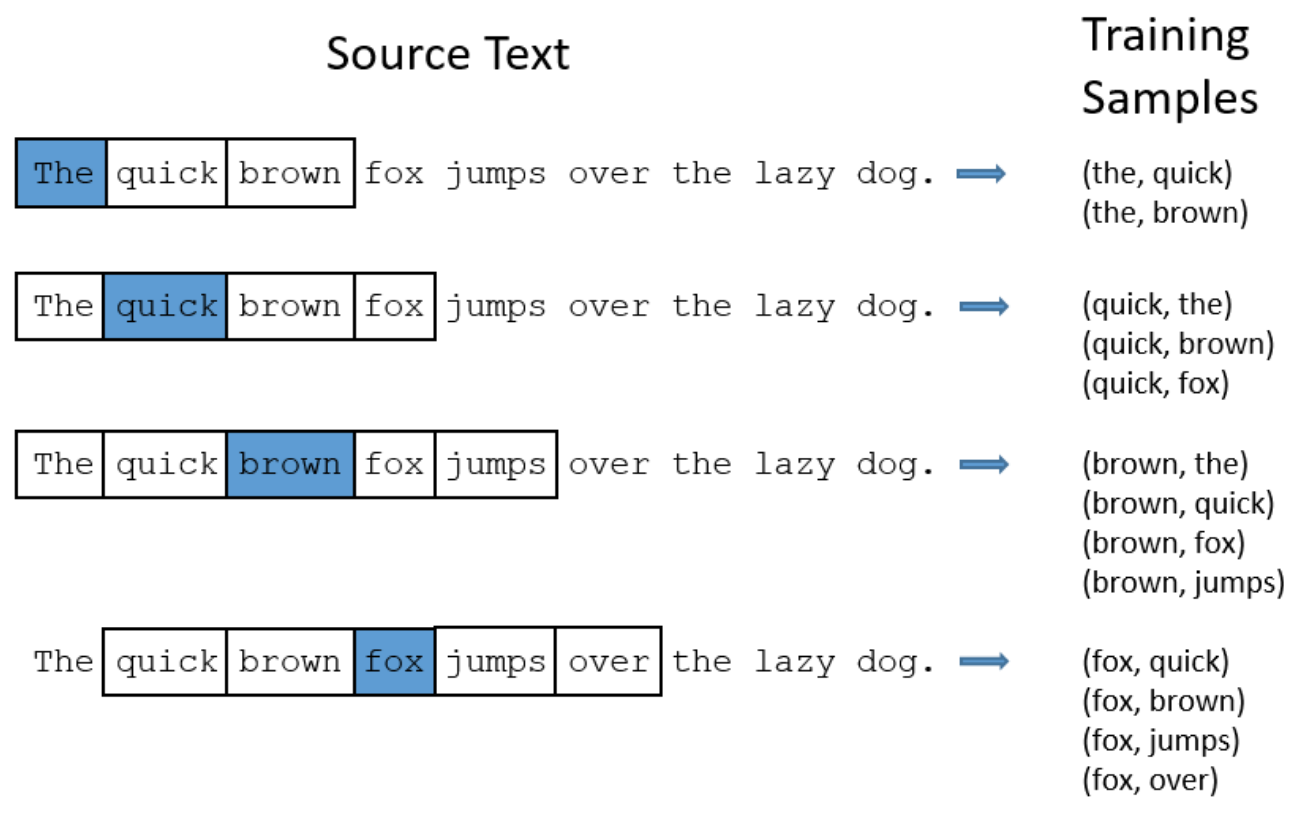
而对Continuous Bag of Words，正好相反。以上图中最后一行为例，

• CBOW: ((quick, brown, jumps, over), fox)
• Skip-Gram: (fox, quick), (fox, brown), (fox, jumps), (fox, over)

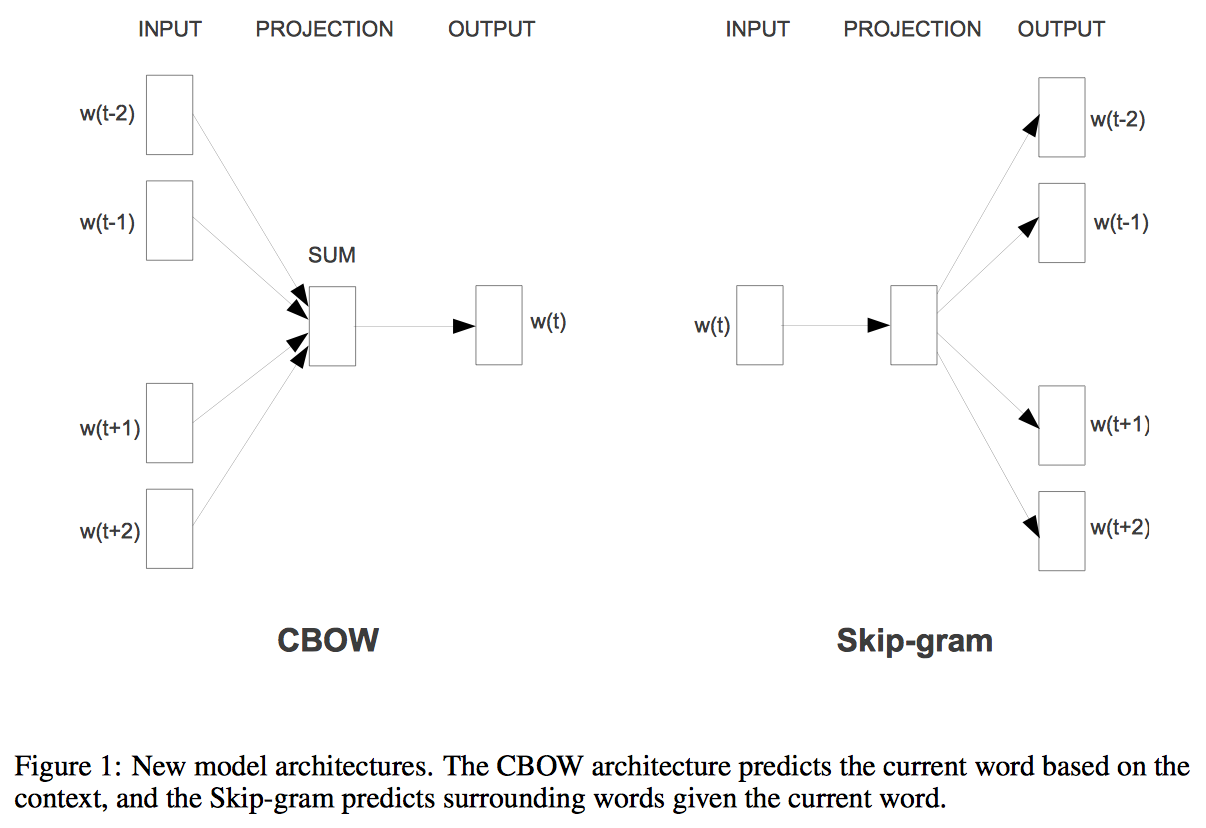
其实根据论文Efficient Estimation of Word Representations in Vector Space中Skip-Gram和CBOW模型结构，理解上述构建样本方式非常的直观。

条件概率计算

Use the similarity of the word vectors for $c$ and $o$ to calculate the probability of $o$ given $c$ (or vice versa).

两个词语的相似度可以用向量內积来表示，但据此如何计算条件概率呢？每一样本对应一条件概率，具体含义如下图：

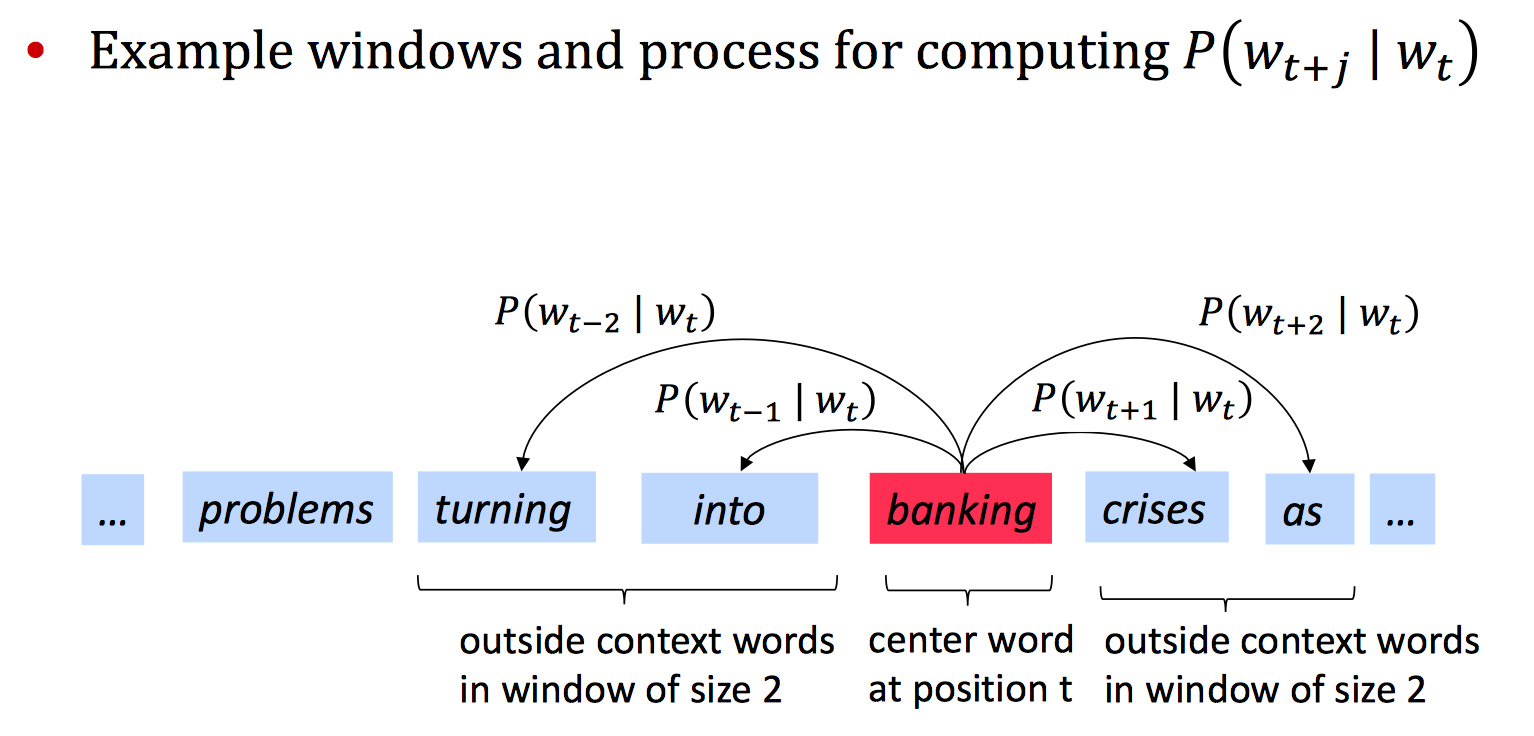
即中心词已知的条件下，context词出现的概率。问题是如何计算$p(w_{t+j}

w_t)$呢？word2vec里思路是将其转化为多分类问题，计算公式如下

$$p(w_O|w_I) = \frac{exp(v'_{w_O}v_{w_I})}{\sum_{w=1}^{W}exp(v'_wv_{w_I})}$$

其中$v_w$和$v_w’$分别是词语$w$的“input”和“output”向量表示。利用向量的內积，內积越大概率越大，然后经过softmax转化为概率值。

概率最大化

Keep adjusting the word vectors to maximize this probability.

利用极大似然估计思想。单个样本对的概率得到之后，在整个训练样本集合上，其似然函数为

$$L(\theta) = \prod_{t=1}^T \prod_{-c\le j \le c; j\ne 0}p(w_{t+j}|w_t; \theta)$$

取负对数，然后平均，即可得到objective function，模型优化目标确定，之后就是典型的优化问题

$$J(\theta) = - \frac{1}{T}L(\theta) = -\frac{1}{T}\sum_{t=1}^{T}\sum_{-c \le j \le c; j\ne 0} log p(w_{t+j}|w_t; \theta)$$

但$p(w_O\vert w_I)$公式中的分母计算量太大，精确计算代价较高。有针对此的优化策略，比如Hierarchical Softmax，再比如Negative Sampling方法

$$p(w_O|w_I) \approx log\delta(v'_{w_o}v_{w_I}) + \sum_{i=1}^k E_{w_i \sim P_n(w)}[log\delta(-v'_{w_i} v_{w_I})]$$

Ref

• Efficient Estimation of Word Representations in Vector Space
• Distributed Representations of Words and Phrases and their Compositionality
• Word2Vec Tutorial - The Skip-Gram Model
• word2vec中的数学原理详解
• Huffman Code - CoolShell